次は、平成３１年度神奈川県高校入試数学の問題です。面白そうな問題だと思うので、皆
さん挑戦してみてください。
下図のように、△ABCは円Ｏに内接し、ＡＢ＝７、ＢＣ＝５、ＣＡ＝８とする。円Ｏの周上の点
Ｐを、ＡＣ⊥ＢＰであるようにとり、ＡＣとＢＰの交点をＱとする。
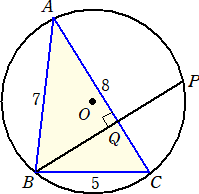
このとき、線分ＢＰの長さを求めよ。
（答） とりあえずの解答です。もっと簡単な解答があったらご教示ください。
（５＋７＋８）/２＝１０ より、ヘロンの公式を用いて、 △ＡＢＣ＝１０
よって、 ８・ＢＱ/２＝１０
より、 ＢＱ＝（５/２）このとき、 ＡＱ＝１１/２ 、 ＱＣ＝５/２
方べきの定理より、 （１１/２）×（５/２）＝（５/２）
×ＰＱ より、 ＰＱ＝（１１/６）以上から、 ＢＰ＝（５/２）
＋（１１/６）＝（１３/３） （終）（コメント） 上記では、△ＡＢＣの面積をヘロンの公式を用いたが、中学生的には次のように
求めるのが標準でしょう。
ＡからＢＣに垂線を下ろし、その垂線の足をＨとおく。ＢＨ＝ｘ とおくと、
４９−ｘ2＝６４−（５−ｘ）2 から、 ｘ＝１ で、 ＡＨ＝４
したがって、 △ＡＢＣ＝５×４
/２＝１０巷間の噂によると、今年度（平成３１年度）の数学は昨年度に比べ、大幅に難化したとの
ことで、確かに、中学生には少し厳しすぎる受験テクニックを要求しているような気がする。
ＰＢさんから別解をいただきました。（平成３１年２月１９日付け）
三平方の定理を用いた、次のような解答もあるかと思いメールしました。
ＣＱ＝ｘ、ＢＱ＝ｙ とおく。
△ＡＢＱについて、 （８−ｘ）＾２＋ｙ＾２＝７＾２ …（１）
△ＢＱＣについて、 ｘ＾２＋ｙ＾２＝５＾２ …（２）
（１）（２）を解いて、 ｘ＝５／２、ｙ＝（５√３）／２
したがって、円周角の定理により、相似な二つの直角三角形△ＡＰＱと△ＢＣＱの辺の比
は、ともに、 １ ： ２ ： √３
ＡＱ＝８−５／２＝１１／２ より、 ＰＱ＝（１１√３）／６
よって、 ＢＰ＝ＢＱ＋ＰＱ＝（１３√３）／２
（コメント） なるほど！方べきの定理を持ち出さなくても辺の比で、ＰＱの長さが求められる
のですね。ＰＢさんに感謝します。
ハンニバル・フォーチュンさんからのコメントです。（平成３１年２月１９日付け）
上記の通り、QB=(5/2)√(3)、QA=11/2、QC=5/2 までが求まったところで、
比例式 QA ： QB=QP ： QC にほうりこめば、QPが求められると思います。
上の比例式は、２つの三角形の相似 △QAB∽△QPC からきています。これが成立する
わけを書きます。
弧BC上の円周角なので、 ∠BAC = ∠BPC
弧AP上の円周角なので、 ∠ABP = ∠ACP
従って、２角相等で、 △QAB ∽ △QPC