
次は、平成31年度神奈川県高校入試数学の問題です。面白そうな問題だと思うので、皆
さん挑戦してみてください。
下図の△ABCにおいて、DはABの中点、E、FはACの3等分点である。BE、BFとCDとの
交点をそれぞれG、Hとおく。
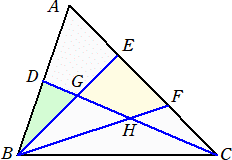
このとき、△BGDの面積と四角形EGHFの面積比を最も簡単な整数比で表せ。
(答) とりあえずの解答です。もっと簡単な解答があったらご教示ください。
メネラウスの定理より、 DG : GC=1 : 4 なので、 △BGD=(1/10)△ABC
同様にメネラウスの定理より、 DH : HC=1 : 1 なので、DG : GH : HC=2 : 3 : 5
よって、 四角形EGHF=(1/3)△ABC−(3/20)△ABC=(11/60)△ABC
以上から、△BGD : 四角形EGHF=(1/10)△ABC : (11/60)△ABC=6 : 11 (終)
HN「愛犬ケン」さんからのコメントです。(平成31年2月16日付け)
メネラウスの定理を使えるのは一部の生徒でしょうね。中学生なので中点連結定理が出
題者の目的でしょうか。
(別解) △ABFで中点連結定理から、DEとBFは平行で、DE:BF=1:2
同様に、△CDEで中点連結定理から、HFとDEは平行で、HF:DE=2:1
よって、HF:DE:BF=1:2:4 すなわち、HF:DE:BH=1:2:3 である。
HF:DE=1:2 から、HはCDの中点となる。
以上から、 DG:GH:HC=2:3:5
よって、 △BDG:△ABC=1:10 、四角形EFHG:△ABC=11:60 となり、
△BDG:四角形EFHG=6:11 (終)
(コメント) 当初、中点連結定理を使う定番の問題だったので、中点連結定理を使おうとは
思いましたが、手っ取り早く DG:GH:HC の比が求められるメネラウスの定理を
使ってしまいました。中学生的には確かに中点連結定理を用いた方が無難でしょ
う。別解をご投稿いただいたHN「愛犬ケン」さんに感謝します。
(追記) 平成31年3月21日付け
最近、次のような別解があることを知った。これも素朴な考え方で中学生が思いつくような
解法と言えるだろう。
(別解) 点Dより、辺ACに平行な直線を引き、線分BE、BFとの交点をそれぞれI、Jとおく。
このとき、△DIGと△CEGは相似なので、DG:GC=1:4=2:8
同様に、△DJHと△CFHは相似なので、DH:HC=1:1=5:5
よって、DG:GH:HC=2:3:5 となる。
そこで、△DBG=6S とおくと、△GBH=9S で、△HBC=15S
よって、 △DBC=6S+9S+15S=30S で、 △ADC=30S
このとき、 △ABE=△EBF=△FBC=20S なので、
四角形EGHF=20S−9S=11S
したがって、 △DBG:四角形EGHF=6S:11S=6:11 (終)