何でもないような問題　　　　　　　 　　　　　　　　　　　　　　　戻る

　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２７年１０月７日付け）

　△ABCで、∠A＝60°、∠B＝20°、AB＝1 のとき、1/AC−BC の値は？







































（答）　DD++さんが考察されました。（平成２７年１０月７日付け）

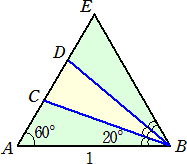　辺 AC の延長上に２点 D、E を、∠CBD=∠DBE=20° とな
るように取る。

　△ABE は一辺が１の正三角形で、△ABC≡△EBD である。

　線分 BC は ∠ABD の二等分線なので、

　　　ＡＢ ： ＢＤ = ＡＣ ： ＣＤ　より、　AC × BD = AB × CD

　　　　　　　　　　　　すなわち、　AC × BC = 1 × (1−２AC)　より、　1 - AC×BC = ２AC

　　　　　　　　　　　　　よって、 1/AC - BC = ２

[別解]　正弦定理より、

　　1/AC = sin100° / sin20° = sin80° / sin20°

　BC = sin60° / sin100° = /(2cos10°)
　　　= sin10° / (2sin10°cos10°) = cos80° / sin20°

　よって、1/AC - BC = (sin80° - cos80°) / sin20°
　　　　　　　　　　　　　= 2sin(80°-60°) / sin20° = 2sin20° / sin20° = 2

＃　初等的でも力技でもさらっと解けますね。AC の延長上にDをとって △ABC∽△ADB と
　するやり方もありそう。