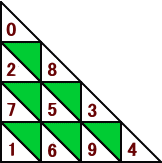
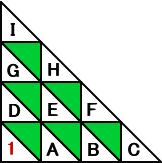
左図において、A〜I には、０から９までの数（ただし、１は除く。）が次の規則にしたがって、重複することなく、一つずつ入るものとする。
（規則） Ｄ〜I のどの数も、
その数の（下の数）と（下の数の右隣の数）の和を１０で割っ
た余りになっている。
すなわち、例えば、Ｇ≡Ｄ＋E（ｍｏｄ １０） が成り立つ。
このとき、A〜I に入る数を求めよ。
（答） この問題のポイントは、I＝０ しかあり得ないということに気がつくことだろう。途中に０が
あると、同じ数が重複するからである。さらに、
D≡1+A、E≡A+B、F≡B+C、G≡D+E、H≡E+F、I≡G+H （以上すべて、ｍｏｄ １０）
において、
Ｇ≡１＋２A＋Ｂ、Ｈ≡A＋２Ｂ＋Ｃ、I≡１＋３A＋３Ｂ＋Ｃ なので、A、Ｂ、Ｃ を決めれば、残り
は確定する。Excel を用いて、実験を行った結果が次の表である。
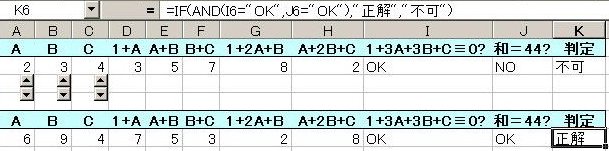
正解と判定される中にも、実は数字の重複する場合が含まれている。その点に関しては、視認
により、解から除外した。上記の解は、唯一無二の正解である。従って、次のように配置される。
