
当HPがいつもお世話になっているHN「りらひい」さんからの出題です。
(令和4年4月7日付け)
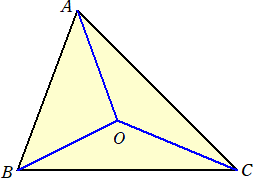
[1] △ABCの各辺(延長線を含む)上にない点Oをとると、
(sin∠ABO / sin∠OBC) * (sin∠BCO / sin∠OCA) * (sin∠CAO / sin∠OAB) = 1
が成り立つことを証明してください。
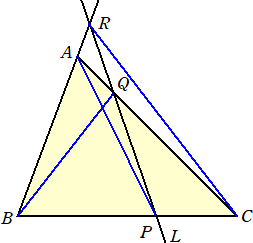
[2] △ABCの各頂点を通らず、かつ、各辺と平行でない直線Lをとり、直線Lと直線BC、直
線CA、直線ABの交点をそれぞれP、Q、Rとすると、
(sin∠ABQ / sin∠QBC) * (sin∠BCR / sin∠RCA) * (sin∠CAP / sin∠PAB) = 1
が成り立つことを証明してください。
(答)[1] △OAB、△OBC、△OCAの高さに着目して、
OAsin∠OAB=OB・sin∠ABO、OB・sin∠OBC=OC・sin∠BCO、OCsin∠OCA=OA・sin∠CAO
これより、 sin∠ABO / sin∠OAB=OA/OB、sin∠BCO / sin∠OBC=OB/OC、
sin∠CAO/ sin∠OCA =OC/OA なので、
(sin∠ABO / sin∠OAB)(sin∠BCO / sin∠OBC)(sin∠CAO/ sin∠OCA )
=(OA/OB)(OB/OC)(OC/OA)=1
よって、 (sin∠ABO / sin∠OBC)(sin∠BCO / sin∠OCA)(sin∠CAO/ sin∠OAB )=1
[2] △QAB、△QBC、△RBC、△RCA、△PCA、△PABの高さに着目して、
QBsin∠ABQ=QAsinA、QBsin∠QBC=QCsinC、RCsin∠BCR=RBsinB、
RCsin∠RCA=RAsinA、PAsin∠CAP=PCsinC、PAsin∠PAB=PBsinB
このとき、
(sin∠ABQ / sin∠QBC)(sin∠BCR / sin∠RCA)(sin∠CAP / sin∠PAB)
=(QAsinA/QB)(QB/QCsinC)(RBsinB/RC)(RC/RAsinA)(PCsinC/PA)(PA/PBsinB)
=(RB/RA)(QA/QC)(PC/PB)
ここで、△ABCにおいて、メネラウスの定理より、 (RB/RA)(QA/QC)(PC/PB)=1
よって、 (sin∠ABQ / sin∠QBC)(sin∠BCR / sin∠RCA)(sin∠CAP / sin∠PAB)=1
出題者のりらひいさんから解答をいただきました。(令和4年4月10日付け)
[1] (解その1)
点Oから三角形ABCの辺BC、CA、ABへおろした垂線の足をそれぞれD、E、Fとすると、
(sin∠ABO / sin∠OBC)(sin∠BCO / sin∠OCA)(sin∠CAO / sin∠OAB)
= ((OF/OB) / (OD/OB))((OD/OC) / (OE/OC))((OE/OA) / (OF/OA)) = 1
(解その2)
正弦定理を使うと、
(sin∠ABO / sin∠OBC)(sin∠BCO / sin∠OCA)(sin∠CAO / sin∠OAB)
= (((AO/AB)sin∠AOB) / ((OC/BC)sin∠BOC))(((BO/BC)sin∠BOC) / ((OA/CA)sin∠COA))
*(((CO/CA)sin∠COA) / ((OB/AB)sin∠AOB)) = 1
(解その3)
(sin∠ABO / sin∠OBC)(sin∠BCO / sin∠OCA)(sin∠CAO / sin∠OAB)
= (((1/2)AB・BOsin∠ABO) / ((1/2)OB・BCsin∠OBC))(((1/2)BC・COsin∠BCO) / ((1/2)OC・CAsin∠OCA))
*(((1/2)CA・AOsin∠CAO) / ((1/2)OA・ABsin∠OAB))
= (△ABO / △OBC) * (△BCO / △OCA) * (△CAO / △OAB) = 1
[2] (解その1)
∠ABQ=∠RBQ または ∠ABQ+∠RBQ=π のいずれかが成り立つことと正弦定理より
sin∠ABQ = sin∠RBQ = (QR/BQ)sin∠BRQ が成り立つ。同様にして、
sin∠QBC = sin∠QBP = (PQ/BQ)sin∠BPQ
sin∠BCR = sin∠PCR = (RP/CR)sin∠CPR
sin∠RCA = sin∠RCQ = (QR/CR)sin∠CQR
sin∠CAP = sin∠QAP = (PQ/AP)sin∠AQP
sin∠PAB = sin∠PAR = (RP/AP)sin∠ARP が成り立つ。
また、∠BPQ=∠CPR または ∠BPQ+∠CPR=π のいずれかが成り立つことなどから、
sin∠BPQ = sin∠CPR 、sin∠CQR = sin∠AQP 、sin∠ARP = sin∠BRQ
もわかる。よって、
(sin∠ABQ / sin∠QBC)(sin∠BCR / sin∠RCA)(sin∠CAP / sin∠PAB)
= (sin∠RBQ / sin∠QBP)(sin∠PCR / sin∠RCQ)(sin∠QAP / sin∠PAR)
= (((QR/BQ)sin∠BRQ) / ((PQ/BQ)sin∠BPQ))(((RP/CR)sin∠CPR) / ((QR/CR)sin∠CQR))
*(((PQ/AP)sin∠AQP) / ((RP/AP)sin∠ARP))
= (sin∠BRQ・sin∠CPR・sin∠AQP) / (sin∠BPQ・sin∠CQR・sin∠ARP) = 1
(解その2)
[1]より、
(sin∠ABQ / sin∠QBP)(sin∠BPQ / sin∠QPA)(sin∠PAQ / sin∠QAB) = 1 …[あ]
(sin∠ACR / sin∠RCP)(sin∠CPR / sin∠RPA)(sin∠PAR / sin∠RAC) = 1 …[い]
が成り立つ。
また、∠QBC=∠QBP または ∠QBC+∠QBP=π のいずれかが成り立つことなどから、
sin∠QBC = sin∠QBP 、sin∠BCR = sin∠RCP 、sin∠BPQ = sin∠CPR
sin∠QPA = sin∠RPA 、sin∠CAP = sin∠PAQ 、sin∠PAB = sin∠PAR
sin∠QAB = sin∠RAC
が成り立ち、これらを[あ]、[い]に代入して、[あ]÷[い]を計算すると、
(sin∠ABQ / sin∠QBC)(sin∠BCR / sin∠RCA)(sin∠CAP / sin∠PAB) = 1
を得る。
(コメント) いろいろな示し方に感動しました。特に、[1]の(解その3)は神懸っていますね。
とても斬新です!
以下、工事中!