
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和3年8月1日付け)
次の連立方程式を解け。
y-x=1 、x^2+y^2=25
(答) y=x+1 を x^2+y^2=25 に代入して整理すると、x^2+x-12=0
(x+4)(x-3)=0 から、x=-4,3
よって、(x,y)=(-4,-3),(3,4) (終)
よおすけさんから別解をいただきました。(令和6年9月30日付け)
y−x=1、x^2+y^2=25 を xy 平面上に表すと、下図のようになる。
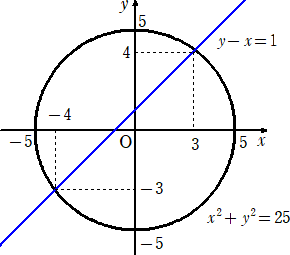
よって、解 (x,y) は、y−x=1、x^2+y^2=25 の交点の座標に等しいので、
(x,y)=(-4,-3),(3,4) (終)