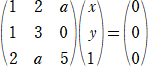当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(平成30年8月7日付け)
次の3直線が1点で交わるような定数aの値を求めよ。
x+2y+a=0 、x+3y=0 、2x+ay+5=0
(答) S(H)さんが考察されました。(平成30年8月7日付け)
Ideal (ring theory)
< x + 2y + a, x + 3y, 2x + ay + 5>= <(-5 + a) (-1 + a), -a + y, 3 a + x>
から、a=5、1
S(H)さんからの続報です。(平成30年8月8日付け)
上記以外に、多様な発想で叶います。
x+2y+a=0 、2x+ay+5=0 の交点 ((10-a^2)/(-4+a),(-5+2 a)/(-4+a)) が
x+3y=0 上にあることから、 -(((-5+a) (-1+a))/(-4+a))=0 より、 a=5、1
(コメント) 高校生風に解けば次のようでしょうか?
x=−3y を第一式、第三式に代入して、 y=a 、(a−6)y+5=0 から、
(a−6)a+5=0 より、 a2−6a+5=0 よって、 a=1、5
高校数学に今は無き行列を用いて、次のような解法(消去法)もあるでしょう。
多分、S(H)さんが一番好きな解法かな?