三角方程式 　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　

　平成２３年１月２日付けで、当ＨＰの掲示板「出会いの泉」に、ＨＮ「ぽっぽ」さんからの出題
です。

　　ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　を満たすθを求めよ。

　高等数学を使うと簡単なので、初等的（知識的には中学数学レベル）で証明してください。



































（答え）　当ＨＰがいつもお世話になっているＨＮ「らすかる」さんが解かれました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１月３日付け）

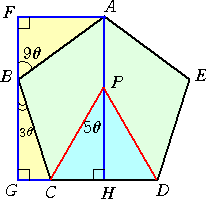
　　一辺が１の正五角形ＡＢＣＤＥの内部に正三角形ＰＣＤ

　を描き、Ｂ、Ｐからそれぞれ直線ＣＤに垂線ＢＧ、ＰＨを下

　ろして長方形ＡＦＧＨを作れば、θ＝６°として、

　　ｓｉｎ９θ＝ＡＦ＝ＧＨ＝ＧＣ＋ＣＨ＝ｓｉｎ３θ＋ｓｉｎ５θ

　が成り立つ。




　θ＝６°のとき、　ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　が成り立つことは、上図から理解される
が、攻略法さんが計算で確認された。（平成２３年１月４日付け）

　ｓｉｎ９θ−ｓｉｎ３θ＝ｓｉｎ５４°−ｓｉｎ１８°

　　　　　　　　　　　 ＝２ｃｏｓ３６°ｓｉｎ１８°（←和積公式）

　　　　　　　　　　　 ＝２ｃｏｓ３６°ｓｉｎ１８°ｃｏｓ１８°/ｃｏｓ１８°

　　　　　　　　　　　 ＝ｃｏｓ３６°ｓｉｎ３６°/ｃｏｓ１８°

　　　　　　　　　　　 ＝ｓｉｎ７２°/（２ｃｏｓ１８°）

　　　　　　　　　　　 ＝ｃｏｓ１８°/（２ｃｏｓ１８°）

　　　　　　　　　　　 ＝１/２

　　　　　　　　　　　 ＝ｓｉｎ３０°＝ｓｉｎ５θ

　　よって、θ＝６°のとき、　ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　が成り立つ。


　さらに、らすかるさんは、解析的な方法により、解を全て求められた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１月３日付け）
（所謂「高等数学」を使った解答）

　　ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　（０°＜θ＜９０°）とする。

　ｎ 倍角の公式（→参照：らすかるさんのＨＰ「らすかるの家」）により、

　　　ｓｉｎ３θ＝−４ｓｉｎ³θ＋３ｓｉｎθ

　　　ｓｉｎ５θ＝１６ｓｉｎ⁵θ−２０ｓｉｎ³θ＋５ｓｉｎθ

　　　ｓｉｎ９θ＝２５６ｓｉｎ⁹θ−５７６ｓｉｎ⁷θ＋４３２ｓｉｎ⁵θ−１２０ｓｉｎ³θ＋９ｓｉｎθ

なので、簡単のため　ｓｉｎθ＝ｘ　とおいて整理すると、

　　２５６ｘ⁹−５７６ｘ⁷＋４１６ｘ⁵−９６ｘ³＋ｘ＝０

０°＜θ＜９０°より、　ｘ＝ｓｉｎθ≠０　としてよいので、両辺を ｘ で割ると、

　　２５６ｘ⁸−５７６ｘ⁶＋４１６ｘ⁴−９６ｘ²＋１＝０

　ここで、Ｆ（ｘ）＝２５６ｘ⁸−５７６ｘ⁶＋４１６ｘ⁴−９６ｘ²＋１　とおくと、グラフは ｙ 軸に関して対

称で、

　　Ｆ（０）＝１＞０　、Ｆ（１/２）＝１−９＋２６−２４＋１＝−５＜０　、

　　Ｆ（３/４）＝６５６１/２５６−６５６１/６４＋１０５３/８−５４＋１＝４４５/２５６＞０

　　Ｆ（１５/１６）＝−５５４９７５９/１６７７７２１６＜０

　　Ｆ（１）＝２５６−５７６＋４１６−９６＋１＝１＞０

となるので、正の実数解は４個ある。


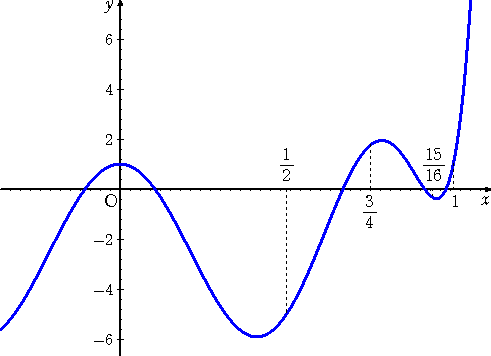
　それぞれの解の近似値をニュートン法で求めると、

　　　0.104528463267653471399834154802…
　　　0.669130606358858213826273330686…
　　　0.913545457642600895502127571985…
　　　0.978147600733805637928566747869…

　これらの値から、θ＝ｓｉｎ^-1ｘ （度数法）を求めると、　約６°、４２°、６６°、７８°

　θ＝６°のとき、 ｓｉｎ３θ＝(−１)/４、ｓｉｎ５θ＝１/２、ｓｉｎ９θ＝(＋１)/４

　θ＝４２°のとき、 ｓｉｎ３θ＝(＋１)/４、ｓｉｎ５θ＝−１/２、ｓｉｎ９θ＝(−１)/４

　θ＝６６°のとき、　ｓｉｎ３θ＝−(−１)/４、ｓｉｎ５θ＝−１/２、ｓｉｎ９θ＝−(＋１)/４

　θ＝７８°のとき、　 ｓｉｎ３θ＝−(＋１)/４、ｓｉｎ５θ＝１/２、ｓｉｎ９θ＝−(−１)/４

となって与式を満たすので、０°＜θ＜９０°の範囲の解は、

　　　θ＝６°、４２°、６６°、７８°

である。

（コメント）　ｓｉｎθの１周期分で解を求めると、

　　　θ＝６°、４２°、６６°、７８°、１０２°１１４°、１３８°、１７４°、

　　　　　１８６°、２２２°、２４６°、２５８°、２８２°、２９４°、３１８°、３５４°

　　　これに、θ＝０°、１８０°も加えて、解は全部で、１８個かな．．．。

　（ぽっぽさんが「高等数学を使うと簡単」と仰ってますが、それほど簡単ではないような．．．雰囲気。）


　当ＨＰがいつもお世話になっているＨＮ「攻略法」さんが斬新な別解を考えられた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１月３日付け）

（別解）　ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　（０＜θ＜π/２）とする。

両辺に、ｃｏｓ３θ（≠０）をかけて、

　　ｓｉｎ３θｃｏｓ３θ＋ｓｉｎ５θｃｏｓ３θ＝ｓｉｎ９θｃｏｓ３θ

２倍角の公式、積和公式より、

　　（１/２）ｓｉｎ６θ＋（１/２）（ｓｉｎ８θ＋ｓｉｎ２θ）＝（１/２）（ｓｉｎ１２θ＋ｓｉｎ６θ）

すなわち、　ｓｉｎ６θ＋ｓｉｎ８θ＋ｓｉｎ２θ＝ｓｉｎ１２θ＋ｓｉｎ６θ　より、

　　　　ｓｉｎ２θ＋ｓｉｎ８θ＝ｓｉｎ１２θ＝ｓｉｎ４θｃｏｓ８θ＋ｃｏｓ４θｓｉｎ８θ

このとき、

　　ｓｉｎ２θ＋ｓｉｎ８θ（１−ｃｏｓ４θ）＝ｓｉｎ４θｃｏｓ８θ＝２ｓｉｎ２θｃｏｓ２θｃｏｓ８θ

ここで、　１−ｃｏｓ４θ＝２ｓｉｎ²２θ　なので、

　　　ｓｉｎ２θ＋２ｓｉｎ８θｓｉｎ²２θ＝２ｓｉｎ２θｃｏｓ２θｃｏｓ８θ

両辺を、ｓｉｎ２θ（≠０）で割って

　　　　　　１＋２ｓｉｎ８θｓｉｎ２θ＝２ｃｏｓ２θｃｏｓ８θ

よって、　２（ｃｏｓ２θｃｏｓ８θ−ｓｉｎ８θｓｉｎ２θ）＝１　すなわち、　ｃｏｓ１０θ＝１/２

　０＜１０θ＜５π　において、　１０θ＝π/３、５π/３、７π/３、１１π/３、１３π/３　より、

　　　θ＝π/３０、π/６、７π/３０、１１π/３０、１３π/３０

　ｃｏｓ３θ≠０　から、　θ＝π/６　は不適。（実際に、θ＝π/６　は解になりえない。）

　以上から、　θ＝π/３０、７π/３０、１１π/３０、１３π/３０　　（終）


　攻略法さんの別解に対して、らすかるさんの補足です。（平成２３年１月４日付け）

　いきなりｃｏｓ３θを両辺にかけるのは思い付かないかも知れませんが、次のような式変形
を考えた場合は、その発想が浮かぶと思います。

　　ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　より、　ｓｉｎ９θ−ｓｉｎ３θ＝ｓｉｎ５θ

　和積公式より、　２ｃｏｓ６θｓｉｎ３θ＝ｓｉｎ５θ

　両辺に、ｃｏｓ３θを掛けて、　２ｃｏｓ６θｓｉｎ３θｃｏｓ３θ＝ｓｉｎ５θｃｏｓ３θ

　　　ｃｏｓ６θｓｉｎ６θ＝ｓｉｎ５θｃｏｓ３θ

　　（１/２）ｓｉｎ１２θ＝（１/２）（ｓｉｎ８θ＋ｓｉｎ２θ）　から、　ｓｉｎ１２θ＝ｓｉｎ８θ＋ｓｉｎ２θ

　　　以下攻略法さんの計算と同じですが、次のようにしても解けます。

　　　　ｓｉｎ１２θ−ｓｉｎ８θ＝ｓｉｎ２θ　より、　２ｃｏｓ１０θｓｉｎ２θ＝ｓｉｎ２θ

　　　よって、両辺を、ｓｉｎ２θ（≠０）で割って、　ｃｏｓ１０θ＝１/２

　　　　これから、θが求められます。

　なお、ＦＮさんによれば、ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θ　を　ｓｉｎ１２θ＝ｓｉｎ８θ＋ｓｉｎ２θ
と変形することは、相当大きな進歩である（平成２３年１月４日付け）とのことですが、らすか
るさんの調査（平成２３年１月４日付け）によれば、上記のような

　　　　「移項→和積→cos掛け→sin２倍角と積和→移項→和積」

という手順の式変形は、　ｓｉｎ３ｋθ＋ｓｉｎ５ｋθ＝ｓｉｎ９ｋθ　のタイプのみに有効とのことで
ある。

（コメント）　攻略法さん、らすかるさん、ありがとうございます。華麗な式変形に感動しました！

　上記の計算では、ｓｉｎ３θ＋ｓｉｎ５θ＝ｓｉｎ９θを式変形して、ｓｉｎ８θ＋ｓｉｎ２θ＝ｓｉｎ１２θ
が導かれたわけであるが、この等式に関連して次のような図形の性質が背景にあることを、
ＦＮさんが指摘された。（平成２３年１月４日付け）

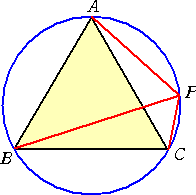　　円に内接する正三角形ＡＢＣの弧ＡＣ上に点Ｐがあるとき、

　　　　　　ＰＢ＝ＰＡ＋ＰＣ

　　が成り立つ。


　　　証明は簡単ではないが、証明そのものは、とても技巧的
　　で美しい！

（証明）　右図のように、ＰＣの延長上に、ＡＰ＝ＣＱ　となる 　　　　点Ｑをとる。このとき、　ＡＢ＝ＣＢ　、　ＡＰ＝ＣＱ　で、 　　　四角形ＡＢＣＰが円に内接することから、 　∠ＰＡＢ＝∠ＱＣＢ　なので、　△ＡＢＰ≡△ＣＢＱ　が成り 立ち、　ＢＰ＝ＢＱ　となる。 　また、　∠ＰＢＱ＝∠ＰＢＣ＋∠ＣＢＱ 　　　　　　　　　　＝∠ＰＢＣ＋∠ＡＢＰ＝６０° であることから、△ＰＢＱは正三角形となる。 　よって、　ＰＢ＝ＰＱ＝ＰＣ＋ＣＱ＝ＰＡ＋ＰＣ　　（証終）

　上図で、∠ＰＡＣ＝１２°にとると、

　　　∠ＰＣＡ＝６０°−１２°＝４８°　、　∠ＰＡＢ＝６０°＋１２°＝７２°

円の直径を１とすると、正弦定理により、

　ＰＡ＝ｓｉｎ∠ＰＣＡ＝ｓｉｎ４８°、ＰＢ＝ｓｉｎ∠ＰＡＢ＝ｓｉｎ７２°、ＰＣ＝ｓｉｎ∠ＰＡＣ＝ｓｉｎ１２°

　よって、　ｓｉｎ４８°＋ｓｉｎ１２°＝ｓｉｎ７２°が成り立ち、θ＝６°とすると、

　　　　ｓｉｎ８θ＋ｓｉｎ２θ＝ｓｉｎ１２θ

を満たす。


　また、

　ｓｉｎＡ＋ｓｉｎＢ＝ｓｉｎＣ　（０°＜Ａ＜Ｂ＜Ｃ＜９０°）を満たす整数 Ａ、Ｂ、Ｃ の組は何
通りあるだろうか？数えられる限りでは３０ですが、他にもありそうだし、それ以外にな
いことも示せないし…

というぽっぽさんの疑問（平成２３年１月４日付け）に対して、らすかるさんによれば、

　「３０個ですべてのようです。

　　(Ａ，Ｂ，Ｃ)＝(ｋ，６０−ｋ，６０＋ｋ) が、ｋ＝１〜２９の２９個と

　　一つだけ特殊な (Ａ，Ｂ，Ｃ)＝(１８，３０，５４)

　で計３０個でした。」

とのことである。（平成２３年１月４日付け）

　実際に、　ｓｉｎｋ＝２ｃｏｓ６０°ｓｉｎｋ＝ｓｉｎ（６０°＋ｋ）−ｓｉｎ（６０°−ｋ）　より、

　　　ｓｉｎｋ＋ｓｉｎ（６０°−ｋ）＝ｓｉｎ（６０°＋ｋ）

がｋの値に依らず成り立つ。

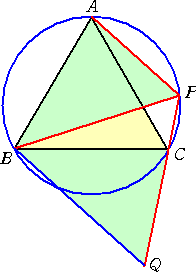
　この(Ａ，Ｂ，Ｃ)＝(ｋ，６０−ｋ，６０＋ｋ) の組合せは、

　　　左図のように直径１の円に内接する正三角形において、

　　ちょうど、　　ＰＣ＝ｓｉｎ∠ＰＡＣ＝ｓｉｎｋ

　　　　　　　　　ＰＡ＝ｓｉｎ∠ＰＢＡ＝ｓｉｎ（６０°−ｋ）

　　　　　　　　　ＰＢ＝ｓｉｎ∠ＰＡＢ＝ｓｉｎ（６０°＋ｋ）

　　であることを考えると興味深い。このことを指摘されたＦＮ

　　さんに感謝したい。（平成２３年１月５日付け）


　また、ＦＮさんは、次の問題を考えられた。

　三角方程式　ｓｉｎａθ＋ｓｉｎｂθ＝ｓｉｎｃθ　が高校数学の範囲で解けるのは、自然
数 ａ、ｂ、ｃ がどのような数であるときか。

　完全な解答を得るのは難しいと思います。ａ＜ｂ　で、ａ、ｂ、ｃ は相異なるものとし、さらに
３数の最大公約数は1は仮定してもいいでしょう。
(ａ＝ｂ は考えてもいいけど、とりあえず考えないとします。)

　まず、和積の公式を使ってただちに出るケースを調べてみました。

　　(１)　このまま和積を使う　　　　　　 　(ａ＋ｂ)/２＝ｃ
　　(２)　さらに右辺に倍角を使う　　　　 (ａ＋ｂ)/２＝ｃ/２　より　ｃ＝ａ＋ｂ

　　　　　　　　　　　　　　　　　　　　　　　　(ｂ−ａ)/２＝ｃ/２　より　ｃ＝ｂ−ａ
　　(３)　ｓｉｎａθ＝ｓｉｎｃθ−ｓｉｎｂθ　として和積を使う　　ａ＝(ｃ−ｂ)/２　より　ｃ＝２ａ＋ｂ
  　　　同様に、　ｓｉｎｂθ＝ｓｉｎｃθ−ｓｉｎａθ より、　ｃ＝ａ＋２ｂ
　　(４)　さらに左辺に倍角を使う　　　　　　 ａ/２＝(ｃ−ｂ)/２　より　ｃ＝ａ＋ｂ　(既出)
　　　　　　　　　　　　　　　　　　　　　　　　　　ａ/２＝(ｂ＋ｃ)/２　 これはない。
  　　　ａとｂを入れ替えても新たなものは出ない。

　以上から、　ｃ＝ｂ−ａ、(ａ＋ｂ)/２、ａ＋ｂ、２ａ＋ｂ、ａ＋２ｂ
　　（これだけでもそこそこあります。）

　　(ａ，ｂ)＝(１，２)　のとき、　ｃ＝３、４、５
　　(ａ，ｂ)＝(１，３)　のとき、　ｃ＝２、４、５、７
　　(ａ，ｂ)＝(１，４)　のとき、　ｃ＝２、３、５、６、９
　　(ａ，ｂ)＝(２，３)　のとき、　ｃ＝１、５、７、９　ｅｔｃ

　これにない中で、ａ、ｂ、ｃ が小さいものは、例えば、ｓｉｎθ＋ｓｉｎ２θ＝ｓｉｎ６θ　とか
ｓｉｎ２θ＋ｓｉｎ３θ＝ｓｉｎ４θ　とかですが、これらは高校数学で解けますか？

　また、これら以外に、高校数学で解ける ａ、ｂ、ｃ の系列はありますか？

(ａ，ｂ，ｃ)＝(３，５，９)の他に特殊な ａ、ｂ、ｃ はあるでしょうか。


　上記に関連して、らすかるさんが考察されました。（平成２３年１月６日付け）

　ｓｉｎθ＋ｓｉｎ２θ＝ｓｉｎ６θ　の方は、解の一つ　θ＝(２/３)π　は比較的簡単に出ました。

（計算）　ｓｉｎθ＋ｓｉｎ２θ＝ｓｉｎ６θ＝２ｓｉｎ３θｃｏｓ３θ

　　　　ｓｉｎθ＋２ｓｉｎθｃｏｓθ＝２ｓｉｎθ（２ｃｏｓθ＋１）（２ｃｏｓθ−１）ｃｏｓ３θ

　　　　（２ｃｏｓθ＋１）｛２（２ｃｏｓθ−１）ｃｏｓ３θ−１｝＝０　（ただし、ｓｉｎθ≠０　とする。）

　　　　　２ｃｏｓθ＋１＝０　から、　θ＝(２/３)π

　　　　　２（２ｃｏｓθ−１）ｃｏｓ３θ−１＝０　から、　

　　　　　　　　２（２ｃｏｓθ−１）（４ｃｏｓ³θ−３ｃｏｓθ）−１＝０

　　　　１６ｃｏｓ⁴θ−８ｃｏｓ³θ−１２ｃｏｓ²θ＋６ｃｏｓθ−１＝０

　　　ここで、　２ｃｏｓθ＝ｘ　とおくと、　ｔ⁴−ｔ³−３ｔ²＋３ｔ−１＝０

　　　　この四次方程式を解くと残りの２解が出せます。


　ｓｉｎ２θ＋ｓｉｎ３θ＝ｓｉｎ４θ　の方は、三次方程式を解けば出ることは出ます。

（計算）　ｓｉｎ２θ＋ｓｉｎ３θ＝ｓｉｎ４θ　より、　ｓｉｎ４θ−ｓｉｎ２θ＝ｓｉｎ３θ

　　　　　２ｃｏｓ３θｓｉｎθ＝ｓｉｎ３θ＝ｓｉｎθ（４ｃｏｓ²θ−１）

　　　　　２ｃｏｓ３θ−４ｃｏｓ²θ＋１＝０　（ただし、ｓｉｎθ≠０　とする。）

　　　　　　よって、　８ｃｏｓ³θ−４ｃｏｓ²θ−６ｃｏｓθ＋１＝０

　　　　　このｃｏｓθに関する三次方程式は、実数解を３個持つが、１個は、１より大きいの

　　　　で不適。残りの２個は、

　　　　　　{１−２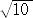ｃｏｓ(ａｒｃｃｏｓ(−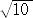/１００)/３)}/６

　　　　　　{１−２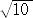ｓｉｎ(ａｒｃｓｉｎ(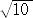/１００)/３)}/６

　　　　なので、答えは、

　　　　　ａｒｃｃｏｓ（{１−２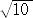ｓｉｎ(ａｒｃｓｉｎ(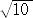/１００)/３)}/６）
　　　　＝1.41460816385035643177…＝81.0510…°

　　　　　ａｒｃｃｏｓ（{１−２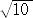ｃｏｓ(ａｒｃｃｏｓ(−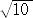/１００)/３)}/６）
　　　　＝2.40475493662310641165…＝137.7823…°


　らすかるさんの考察に対して、ＦＮさんのコメントです。（平成２３年１月６日付け）

　両方とも逆三角関数を使えば解けるということですね。高校数学の範囲でとなるとやはり
無理ですか。前に書いた系列の ａ、ｂ、ｃ 以外にはあまりないのかもしれません。でも、もう
すこしはありそうな気もします。今のところでは、３、５、９が孤立した特異なケースということ
になります。


　さらに、ＦＮさんからの提言です。（平成２３年１月７日付け）

　三角方程式　ｓｉｎａθ＋ｓｉｎｂθ＝ｓｉｎｃθ　が高校数学の範囲で解けるのは、自然
数 ａ、ｂ、ｃ がどのような数であるときか。

について、方法(及び結果)に対する制限より結果に対する制限のほうがいいと思うので、次
のようにしたほうがいいようです。

　三角方程式　ｓｉｎａθ＋ｓｉｎｂθ＝ｓｉｎｃθ　の解がすべてπの有理数倍であるのは、
相異なる自然数 ａ、ｂ、ｃ がどのような数であるときか。
　ただし、ａ＜ｂ、とする。（必要に応じて、ａ、ｂ、ｃ の最大公約数は１とする。）

　多少違うかもしれませんが、ほぼ同じかなと思います。

　ぽっぽさんが提示された次の問題：

　ｓｉｎＡ＋ｓｉｎＢ＝ｓｉｎＣ　（０°＜Ａ＜Ｂ＜Ｃ＜９０°）を満たす整数 Ａ、Ｂ、Ｃ の組は何
通りあるだろうか？

の整数を有理数に変えます。

　ｓｉｎＡ＋ｓｉｎＢ＝ｓｉｎＣ　（０°＜Ａ＜Ｂ＜Ｃ＜９０°）を満たす有理数 Ａ、Ｂ、Ｃ が存在
するのはどのような場合か？

　弧度法で表記すれば、

　ｓｉｎＡ＋ｓｉｎＢ＝ｓｉｎＣ　（０＜Ａ＜Ｂ＜Ｃ＜π/２）を満たす Ａ、Ｂ、Ｃ がπの有理数倍
であるのはどのような場合か？

　前に、ｓｉｎａθ＋ｓｉｎｂθ＝ｓｉｎｃθ　が簡単に解ける場合として、

　　　　ｃ＝ｂ−ａ、(ａ＋ｂ)/２、ａ＋ｂ、２ａ＋ｂ、ａ＋２ｂ

を書きましたが、この中で、上記を満たすＡ、Ｂ、Ｃを生みだすのは、ｃ＝２ａ＋ｂ　だけです。
そして、その解は、Ａを　０＜Ａ＜π/６　を満たすπの有理数倍として、

　　B＝π−A　、　C＝π＋A

です。即ち、前にらすかるさんが書かれた　(ｋ，６０−ｋ，６０＋ｋ) 　のタイプです。今のところ
このタイプ以外は、(Ａ，Ｂ，Ｃ)＝(π/１０，π/６，３π/１０)　だけです。


　らすかるさんが、ｃ＝２ａ＋ｂ　以外でπの有理数倍になるものを探されました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１月８日付け）

　有理数は多いので、分母≦３６０　の範囲に限定します。その結果、

　　　　　(Ａ，Ｂ，Ｃ)＝(π/１０，π/６，３π/１０)　だけ

しかありませんでした。

　ｓｉｎａπ＋ｓｉｎｂπ＝ｓｉｎｃπ　（０＜ａ＜ｂ＜ｃ＜１/２、ｃ≠２ａ＋ｂ、ａ、ｂ、ｃは有理数）の解は

　　　　　(１/１０，１/６，３/１０)

のみかも知れませんね。


　らすかるさんの考察に対して、ＦＮさんのコメントです。（平成２３年１月８日付け）

　その可能性はありそうですね。証明できそうな気はしませんが．．．。

　ｓｉｎａπ＋ｓｉｎｂπ＝ｓｉｎｃπ　で有理数 ａ、ｂ、ｃ の共通分母 ｎ をとって、

　　　　　ｓｉｎ（ａ’/ｎ）π＋ｓｉｎ（ｂ’/ｎ）π＝ｓｉｎ（ｃ’/ｎ）π　と書く。

　このことから、１のｎ乗根 ω＝ｃｏｓ(π/ｎ)＋ｉ・ｓｉｎ(π/ｎ)　とおくと、　ω^a’＋ω^b’−ω^c’
が実数になる条件を求めることになる。円分体についての高度な理論を使えばできるかも
しれない。



　　　　　　以下工事中