分割パズル（７）　　　　　　　　　　　　　　　　　　　　　　　　

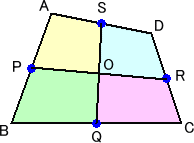
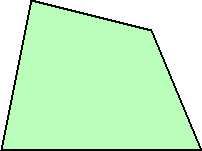
左図のような四角形を、５個の小図形に分割し、 　　　それらを組み合わせて１つの長方形を作りたい。 　　　　どうしたらよいだろうか？

（答）　次のように分割すればよい。

　　　　　　　　　　　　　　　

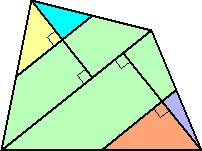
　　これらを組み合わせて、次のような長方形ができる。

　　　　　　　　　　　　　　　　　

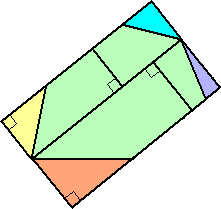
　この問題は、任意の四角形で可能であることが興味を引くところである。

（追記）　平成２２年３月１０日付け

　　当ＨＰの掲示板「出会いの泉」で、ＨＮ「Ｈ．Ｉ．」さんより、４個の小図形に分割し、それら
　を組み合わせて１つの長方形が作れることをご教示いただいた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２２年２月２７日付け）

　　　　　　　　　　　　　　　

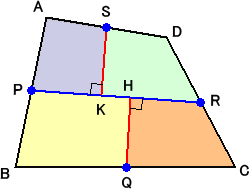
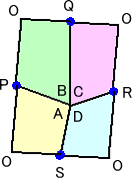
　　４つの中点の１つを選んで、鳩目返しをすると、長方形が得られるとのことである。

（追記）　平成２２年９月２９日付け

　　上記のＨＮ「Ｈ．Ｉ．」さんよりご教示いただいた方法は、あの安土桃山時代の豊臣秀吉に
　よる太閤検地の方法であることを、平成２２年９月２５日付けの朝日新聞夕刊で知ることが
　できた。（参考：　大井康嗣さんの公開授業（酒田市立松原小学校））

　　ＰＲ＝ａ　、ＱＨ＝ｘ　、ＳＫ＝ｙ　とおくと、四角形の面積Ｓは、Ｓ＝ａ（ｘ＋ｙ）　で与えられる。

　実際には、　ｘ＝ｙ　なので、　Ｓ＝２ａｘ　である。

　（ｘ＝ｙ　であることの証明）　４つの中点の１つを選んで鳩目返しをすると長方形

　　　　　　　

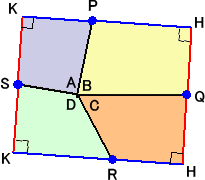
　　が得られることから明らかだろうが、幾何的には次のようにして示される。

　　　各辺の中点を結ぶ四角形ＰＱＲＳは中点連結の定理により平行四辺形となる。

　　この平行四辺形の面積は対角線ＰＲにより２等分される。

　　このとき、　ＰＲ＝ａ　、ＱＨ＝ｘ　、ＳＫ＝ｙ　とおくと、

　　　　　ａｘ/２＝ａｙ/２　より、　ｘ＝ｙ　が成り立つ。　（証終）

　どんなに不等辺な四角形でも、対辺の中点を結ぶ長さと、中点から下ろした垂線の長さを
測るだけで、面積が正確に測量できることを安土桃山時代の人々が知っていたことに驚か
される。


（追記）　平成２８年９月１６日付け

　上図では特殊な分割をしたが、もっと素朴に次のように分割すれば、４個の小図形を組み
合わせて１つの長方形を作ることは可能である。

　各辺の中点を結んで、各小四角形を中点の周りに回転させて長方形が出来る。