ダビデの星 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　戻る

　　　ダビデの星は、２つの正三角形（△，▽）を重ね合わせたものである。イスラ
　　エルの国旗にも使われている。
　　△は、男性（火）、▽は、女性（水）を表す。両者の重なり（共同体）が、地球を
　　表すという。

　このページでは、ダビデの星に因んで、下記のような魔方陣を考える。

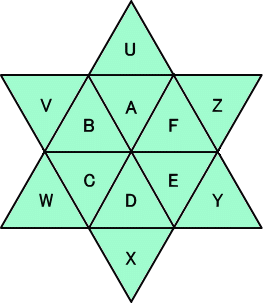　　　右斜め、左斜め、横の数の和がそれぞれ一

　　定になるように、Ａ〜Ｆ、Ｕ〜Ｚに、１から１２ま

　　での自然数をすべて配置せよ。

　　即ち、　　Ｕ＋Ａ＋Ｂ＋Ｃ＋Ｗ
　　　　　　＝ Ｚ＋Ｆ＋Ｅ＋Ｄ＋Ｘ
　　　　　　＝Ｕ＋Ａ＋Ｆ＋Ｅ＋Ｙ
　　　　　　＝Ｖ＋Ｂ＋Ｃ＋Ｄ＋Ｘ
　　　　　　＝Ｖ＋Ｂ＋Ａ＋Ｆ＋Ｚ
　　　　　　＝Ｗ＋Ｃ＋Ｄ＋Ｅ＋Ｙ
　　　　　　＝一定


























（答） 　この魔方陣は、当ＨＰの読者である千代原福太郎 様が２０年来気になっているとい
　　　　う六芒星陣である。今回この星陣を考える機会を与えていただいた千代原 様に感謝
　　　　したい。

　まず、１から１２までの自然数の総和は、１２(１＋１２)/２＝７８　であることに注意する。

そこで、ダビデの星の中央の６個の和を Ｓ 、右斜め（左斜め、横）の数の和を　Ｔ　とおく。

　即ち、　　Ｓ＋（ Ｕ＋Ｖ＋Ｗ＋Ｘ＋Ｙ＋Ｚ ）＝７８

　　　　 　 ３Ｓ＋２（ Ｕ＋Ｖ＋Ｗ＋Ｘ＋Ｙ＋Ｚ ）＝６Ｔ

が成り立つ。よって、Ｓ＝６Ｔ−１５６　即ち　Ｔ＝(Ｓ/６)＋２６　である。

　Ｔ は整数なので、Ｓ は、６ の倍数となる。

　　１＋２＋３＋４＋５＋６≦Ｓ≦７＋８＋９＋１０＋１１＋１２　即ち　２１≦Ｓ≦５７　なので、

　Ｓ のとりうる値は、Ｓ＝２４、３０、３６、４２、４８、５４　の ６ 通りある。

このとき、Ｔ ＝３０、３１、３２、３３、３４、３５　である。

　また、　　 Ｕ＋Ａ＋Ｂ＋Ｃ＋Ｗ＝Ｔ　と　 Ｚ＋Ｆ＋Ｅ＋Ｄ＋Ｘ＝Ｔ　を辺々加えて、

　　　Ｕ＋Ｗ＋Ｚ＋Ｘ＋Ａ＋Ｂ＋Ｃ＋Ｄ＋Ｅ＋Ｆ＋Ｗ＝２Ｔ　即ち、

　　　　　　　　　　Ｕ＋Ｗ＋Ｚ＋Ｘ＝２Ｔ−Ｓ

同様にして、
　　　　　　　　　　Ｕ＋Ｙ＋Ｖ＋Ｘ＝２Ｔ−Ｓ
　　　　　　　
　　　　　　　　　　Ｖ＋Ｚ＋Ｗ＋Ｙ＝２Ｔ−Ｓ

したがって、Ｕ＋Ｘ＝Ｖ＋Ｙ＝Ｗ＋Ｚ　が成り立つ。

そこで、Ｕ＋Ｘ＝Ｋ　とおくと、Ｓ＋３Ｋ＝７８　より、Ｋ＝２６−(Ｓ/３)　となる。

　以上から、回転と対称移動により重なるものは同じものとみなして、相異なるもので、起こ

り得る全ての場合を数え上げると、次の表のようになる。

Ｓ ２４ ３０ ３６ ４２ ４８ ５４
Ｔ ３０ ３１ ３２ ３３ ３４ ３５
Ｋ １８ １６ １４ １２ １０ 　８
場合の数 １４４ ２８８ １２２４ １０８０ ３６０ １４４
　　計　３２４０通り

　これら全てを検証した結果、条件を満たす場合は存在して、解は、２個あることが分かっ
た。（検証作業には、表計算ソフト Ｅｘｃｅｌ の ＶＢＡ を利用）　解は次の通りである。

Ｔ＝３３　の場合 Ｔ＝３２　の場合
　
　 　

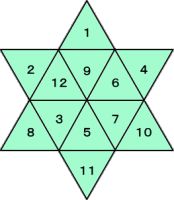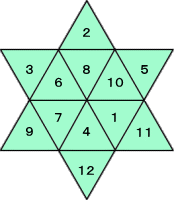（コメント）：　当初の検証では解が１個としてあったが、その後、当ＨＰでも大変お世話にな

　　　　　　っている未菜実さん（数理パズル入門）から、解は２個ある旨のご指摘を頂いた。

　　　　　　上記の検証作業を再チェックしたところ、数えもれの場合が発見され、再検証し

　　　　　　た結果、未菜実さんより頂いた解がもれていたことを確認した。したがって、場合

　　　　　　の数として、１４４通りを追加し、計３２４０通りと訂正します。

　　　　　　大変貴重なご指摘を頂いた未菜実さんに感謝します。（平成１５年１２月２６日記）


（追記）　求め方を一つ例示しておこう。

　　Ｓ＝４２、Ｔ＝３３、Ｋ＝１２　の場合を考える。

　Ｋ＝１２　なので、方程式　Ｍ＋Ｎ＝１２　の解（Ｍ，Ｎ）は、

　　　　　　（１，１１）、（２，１０）、（３，９）、（４，８）、（５，７）

の５通りある。これらから異なる３個の組を選ぶ方法の数は、5Ｃ3＝１０ 通り。

このうちの１通り、例えば、（１，１１）、（２，１０）、（４，８）　について、

｛ Ｖ、Ｙ ｝，｛ Ｗ、Ｚ ｝　のそれぞれの順列を考えて、２×２＝４　通りある。

このうちの１通り、例えば、

　　　（ Ｕ ， Ｘ ）＝（１，１１）、（ Ｖ ， Ｙ ）＝（２，１０）、（ Ｗ ， Ｚ ）＝（８，４）

とする。残っている数は、３、５、６、７、９、１２　の６個ある。

　このとき、Ａ＋Ｆ＋Ｅ＝Ｔ−（Ｕ＋Ｙ）＝３３−（１＋１０）＝２２　なので、

　　　　Ａ ， Ｆ ， Ｅ　のとりうる値は、　３ ， ７ ， １２　　または　　６ ， ７ ， ９

の２通りある。　　したがって、

　　　｛ Ａ ， Ｆ ， Ｅ ｝＝｛ ３ ， ７ ， １２ ｝　、　｛ Ｂ ， Ｃ ， Ｄ ｝＝｛ ５ ， ６ ， ９ ｝

または

　　　｛ Ａ ， Ｆ ， Ｅ ｝＝｛ ６ ， ７ ， ９ ｝　、　｛ Ｂ ， Ｃ ， Ｄ ｝＝｛ ３ ， ５ ， １２ ｝

となる。これらについて、条件を満たすものを探せばよい。

（ Ａ ， Ｆ ， Ｅ ）＝（ ９ ， ６ ， ７ ）　、　（ Ｂ ， Ｃ ， Ｄ ）＝（ １２ ， ３ ， ５ ）　の場合がちょうど

条件を満たす。

（コメント）　条件を満たす場合が複数あるだろうという予想のもとに計算を始めたのですが、
　　　　　　やはり、解は複数個あって、「ホッ！」としました。でも、検証作業に数えもれがあ
　　　　　　って、「本当に解は２個だけ？」という心配はあります。未菜実さんによる検証で、
　　　　　　２個あったということは、それ以上ないということも仰っているということで少し安心
　　　　　　できるかな？