チョコレートの分割 　　　　　　　　　　　　　　　　　　

左図のようなサイズが ３×４ の板チョコがある。この板チョコを溝に 　沿って２つの断片に分ける。チョコレートを重ねて断片に分けることは 　しないとき、最後に１２個の断片にするには、どのような切り方をしても 　必ず１１回の操作が必要であることは明らかだろう。

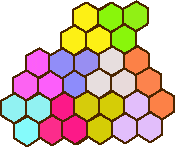
　そこで、問題です。今、１２個の正６角形をつなぎ合わせた形のチョコレートがある。

　　　　

このチョコレートを４人で分けたい。ただし、分割の形は、次の２種類に限定し、回転してもよ
く、それぞれの個数は適当でよいものとする。

　　　　　　　

　果たして、チョコレートの分割は可能だろうか？






















（答）　不可能である。

　元のチョコレートの１２個の部分に ａ、ｂ、ｃ を割り振り、２種類の図形をどこから切り出し
ても ａ、ｂ、ｃ が１個ずつ含まれるようにする。

　　　　

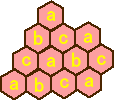
このとき、ａ が５個、ｂ が３個、ｃ が４個であるので、２種類の形でどう切り分けても矛盾が
生じる。２種類の形で切り分け可能とすると、ａ、ｂ、ｃ は同数でなければならないからであ
る。


（コメント）　チョコレートの数が少ないので、不可能なことは瞬殺かな？


　読者のために練習問題を残しておこう。

練習問題　　３０個の正６角形をつなぎ合わせた形のチョコレートがある。

　　　　

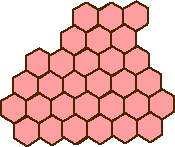
このチョコレートを１０人で分けたい。ただし、分割の形は、次の２種類に限定し、回転しても
よく、それぞれの個数は適当でよいものとする。

　　　　　　　

　果たして、チョコレートの分割は可能だろうか？可能ならば、どのように分割すればいいの
だろうか？


（解）　元のチョコレートの３０個の部分に ａ、ｂ、ｃ を割り振り、２種類の図形をどこから切り
　　　出しても ａ、ｂ、ｃ が１個ずつ含まれるようにする。

　　　　

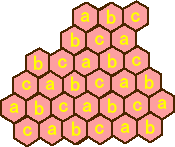
このとき、ａ が１０個、ｂ が１０個、ｃ が１０個であるので、２種類の形での切り分けができそ
うである。（ａ、ｂ、ｃ が同数であっても切り分けが出来ない可能性があるかもしれないが、ま
だ確認していない．．．。）

　実際に、切り分けてみると、一例として、