
チェスのナイトという駒は、将棋の桂馬のような動き方をする。
ただし、ナイトの方が自由度が高い。下図の中央にあるナイトは、○印の部分の何れかに
動くことが出来る。
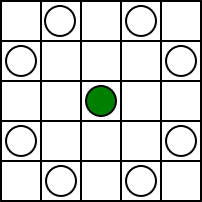
そこで、次のような問題を考える。
下図のような 4×4のチェス盤上のどこかにナイトが1個置いてある。どのマスも2回通る
ことはないものとして、移動できなくなるまで、最大何手かかるだろうか?

(答) 四隅のどれかから出発するのが最大で、14手(多分?)。
他の場所では、せいぜい13手。
ナイトの動きうるマスの相関図は次の通りである。
埋め込みパズル(2) 
チェスのナイトという駒は、将棋の桂馬のような動き方をする。
ただし、ナイトの方が自由度が高い。下図の中央にあるナイトは、○印の部分の何れかに
動くことが出来る。

そこで、次のような問題を考える。
下図のような 4×4のチェス盤上のどこかにナイトが1個置いてある。どのマスも2回通る
ことはないものとして、移動できなくなるまで、最大何手かかるだろうか?

(答) 四隅のどれかから出発するのが最大で、14手(多分?)。
他の場所では、せいぜい13手。
ナイトの動きうるマスの相関図は次の通りである。
 |
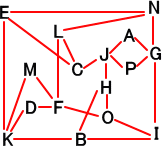 |
ナイトの動き方の例を一つあげる。

(どうしても1マスが余ってしまうのですが、相関図を眺めていると、これはしょうがないこと
ですよね!?)
上の相関図は少し込み入っていて美しさが感じられないが、未菜実の数理パズル入門
の中の「ナイトの周遊」−「更に問題」−「こたえ」で、この相関図が美しく書き上げられてい
る。
相関図は全ての関係が網羅されていて煩雑であるが、いくつかの関係を断ち切れば、別
の美しい関係が浮かび上がってくる。16個のマスが1つの数珠つなぎになるのである。
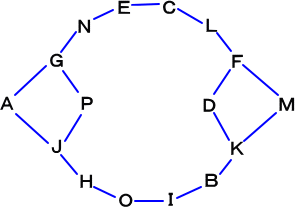
(参考ホームページ:未菜実の数理パズル入門)
(追記) 移動可能な文字間が長さの等しい紐で2本または3本または0本で結ばれている
ものとする。このとき、最長となるパターンは、例えば、次のような場合である。
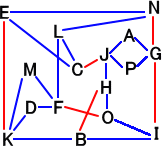 |
左図の位置関係を書き直して、下図を得る。 |
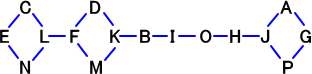 |