
丂僀儞僪偺悢妛幰偵丄僽儔儅僌僾僞乮598乣660乯偲偄偆恖偑偄傞丅斵偼丄師偺傛偆側栤戣傪巆偟偰
偄傞丅乮尨戣偼偡傋偰暥帤偱昞偝傟偰偄傞丅乯
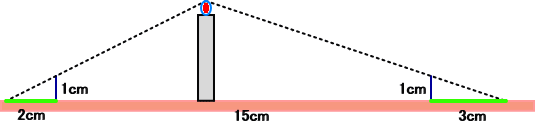
丂侾俆們倣妘偨偭偨強偵丄挿偝 侾們倣偺朹偑悅捈偵棫偰傜傟偰偄傞丅偄傑丄俀偮偺朹偺娫偺揔摉
側強偵丄挿偝偑暘偐傜側偄儘僂僜僋傪偍偄偰丄柧偐傝傪摂偟偨傜丄壓恾偺傛偆側挿偝偺塭偑偱偒
偨丅偙偺偲偒丄儘僂僜僋偺挿偝偼丄偄偔傜偩傠偆偐丠乮墛偺晹暘偺挿偝偼柍帇偡傞傕偺偲偡傞丅乯
丂丂
乮嶲峫暥專丗僐儘僜僼丂挊丂嶳嶈丂徃丒杚栰嬥懢榊丂栿丂悢妛壽奜傛傒傕偺乮嘥乯丂乮搶嫗恾彂乯乯
乮摎乯丂係們倣
丂丂幚嵺偵丄傠偆偦偔偺挿偝傪丄倶 們倣丄嵍懁偺朹偐傜傠偆偦偔傑偱偺嫍棧傪丄倷 們倣偲偡傞偲丄
丂塃懁偺朹偐傜傠偆偦偔傑偱偺嫍棧偼丄侾俆亅倷 們倣偵側傞偺偱丄憡帡嶰妏宍偺曈偺斾偺
丂娭學偐傜丄
丂丂丂丂丂丂丂丂丂丂丂丂丂俀 丗 侾 亖 俀亄倷 丗 倶丂偡側傢偪丄丂俀倶亖俀亄倷
丂丂丂丂丂丂丂丂丂丂丂丂丂俁 丗 侾 亖 侾俉亅倷 丗 倶丂偡側傢偪丂俁倶亖侾俉亅倷
丂丂丂俀偮偺幃傪曈乆壛偊偰丄丂俆倶亖俀侽
丂傛偭偰丄倶亖係乮們倣乯丂偱偁傞丅
丂堦斒偵丄朹偺挿偝傪 倛丄塭偺挿偝傪 倎 丄 倐 丄 俀偮偺朹偺娫妘傪 倓 偲偡傞偲丄
傠偆偦偔偺挿偝 倶 偼丄
丂丂丂丂丂丂丂丂丂丂丂丂倶 亖 倛(倎亄倐亄倓)/(倎亄倐)
偱梌偊傜傟傞丅
乮捛婰乯丂忋婰偺栤戣傪丄摉俫俹撉幰偺俰丏倄丏偝傫偑峫嶡偝傟偨丅乮暯惉俀俁擭侾俀寧俁侽擔晅偗乯
丂丂丂丂
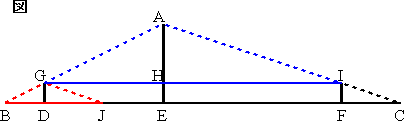
丂恾偺傛偆偵揰偵柤慜傪偮偗傑偡丅偙偙偱丄巐妏宍俧俢俥俬偼挿曽宍偱丄俧俬
傢偐傝傑偡丅
丂偝傜偵丄俧俰
妏乯偲側傝丄傑偨丄暯峴偱偁傞偙偲偐傜丄仮俧俛俰佷仮俙俧俬乮俀慻偺妏乯偱丄偦偺憡帡斾偼丄
丂丂俀亄俁 丗 侾俆 亖 侾 丗 俁
偵側傝傑偡丅憡帡側恾宍偺懳墳偡傞晹暘偺挿偝偺斾偼摍偟偄偺偱丄俧俢 丗 俙俫 亖 侾 丗 俁
丂偙偙偱丄俧俢亖侾乮們倣乯 傛傝丄俙俫亖俁乮們倣乯 偲側傝丄丂俙俤亖俁亄侾亖係乮們倣乯丂偵側傝傑偡丅
丂堦斒偵丄
丂丂俧俢亖俬俥亖倛乮亖俫俤乯丄俛俢亖倎 丄俥俠亖倐 乮亖俢俰乯丄俢俥亖倓乮亖俧俬乯丄俙俤亖倶丂偲偡傞偲丄
丂仮俧俛俰佷仮俙俧俬傛傝丄丂倛 丗 倶亅倛 亖 倎亄倐 丗 倓丂偑惉傝棫偮丅
丂傛偭偰丄乮倎亄倐乯乮倶亅倛乯亖倓倛丂傛傝丄丂倶亅倛亖倓倛乛乮倎亄倐乯丂偐傜丄倶亖倛亄倓倛乛乮倎亄倐乯
偡側傢偪丄丂 倶亖倛亄倛丒倓乛乮倎亄倐乯丂偲側傝傑偡丅
乮僐儊儞僩乯丂俰丏倄丏偝傫丄暿夝傪偄偨偩偒丄偁傝偑偲偆偛偞偄傑偡丅仮俧俛俰 傪峫偊傞偺偑僐僣偺
丂丂丂丂丂丂傛偆偱偡偹両
乮捛婰乯丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俽乮俫乯乿偝傫偑丄忋婰偺栤戣傪峫嶡偝傟偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俁擭侾俀寧俁侾擔晅偗乯
丂丂丂丂

丂嵍塃偐傜岝傪偁偰傞偲丄塭偺挿偝=h 偑嫟捠偱偁傞偙偲偵拲堄偟偰丄
丂俢俤亖倶1 丄俤俥亖倶2 偲偍偔偲丄丂倶1 + 倶2 = 15丂偱丄
丂丂併[(2 + 倶1)2 + h2]丒1/併[22 + 12] = h丂丄併[(倶2 + 3)2 + h2]丒1/併[12 + 32] = h
丂偙偺偲偒丄丂(2 + 倶1)2 = 4h2丂丄(倶2 + 3)2 = 9h2丂傛傝丄丂9(2 + 倶1)2 = 4(倶2 + 3)2
丂倶2 = 15 - 倶1丂傪戙擖偟偰丄丂9(2 + 倶1)2 = 4(18 - 倶1)2
丂場悢暘夝偟偰丄丂乮42 + 倶1乯乮-30 + 5倶1乯 = 0丂傛傝丄丂倶1亖-42丂丄6
丂倶1亜0丂側偺偱丄丂倶1亖-42丂偼晄揔丅丂傛偭偰丄丂倶1亖6
丂偙偺偲偒丄丂倶2亖9丂丄倛亖4
乮仺丂嶲峫丗乽僽儔儅僌僾僞乿乯
丂峌棯朄偝傫偑丄庬乆偺夝朄傪惍棟偝傟傑偟偨丅乮暯惉俀係擭侾寧俀擔晅偗乯
丂壓恾偵偍偄偰丄俧俰
丂俧俢亖俬俥亖倛乮亖俫俤乯丄俛俢亖倎 丄俥俠亖倐 乮亖俢俰乯丄俢俥亖倓乮亖俧俬乯丄俙俤亖倶丂偲偡傞丅
丂丂丂丂

偦偺侾丂丒丒丒丂憡帡嶰妏宍偺挿偝偺斾
丂丂丂丂丂丂丂仮AGI佷仮ABC丂側偺偱丄懳墳偡傞挿偝偵偍偄偰丄
丂丂丂丂丂丂丂掙曈 丗 崅偝 = GI 丗 AH = BC 丗 AE丂傛傝丄 d 丗 倶 - 倛 = 倎 + 倓 + 倐 丗 倶
丂丂丂丂丂丂丂傛偭偰丄丂倶 = 倛(倎 + 倐 + 倓)/(倎 + 倐)
偦偺俀丂丒丒丒丂憡帡嶰妏宍偺挿偝偺斾
丂丂丂丂丂丂丂仮GBJ佷仮ABC側偺偱丄懳墳偡傞挿偝偵偍偄偰丄
丂丂丂丂丂丂丂掙曈 丗 崅偝 = BJ 丗 GD = BC 丗 AE丂傛傝丄丂倎 + 倐 丗 倛 = 倎 + 倓 + 倐 丗 倶
丂丂丂丂丂丂丂傛偭偰丄丂倶 = 倛(倎 + 倐 + 倓)/(倎 + 倐)
偦偺俁丂丒丒丒丂柺愊
丂丂丂丂丂丂丂柺愊偵拲栚偟偰丄丂仮GBD + 仩GDFI + 仮ICF + 仮AGI = 仮ABC丂傛傝丄
丂丂丂丂丂丂丂丂倎倛/2 + 倓倛 + 倐倛/2 + 倓(倶 - 倛)/2 = (倎 + 倐 + 倓)倶/2
丂丂丂丂丂丂丂傛偭偰丄丂倶 = 倛(倎 + 倐 + 倓)/(倎 + 倐)
偦偺係丂丒丒丒丂憡帡嶰妏宍偺柺愊斾
丂丂丂丂丂丂丂仮GBJ佷仮ABC丂偱丄掙曈偺斾偑丂倎 + 倐 丗 倎 + 倓 + 倐丂傛傝丄柺愊斾偼丄
丂丂丂丂丂丂丂丂乮倎 + 倐乯2 丗 乮倎 + 倓 + 倐乯2
丂丂丂丂丂丂丂傛偭偰丄丂(倎 + 倐)倛/2丒乮倎 + 倓 + 倐乯2/乮倎 + 倐乯2 = (倎 + 倓 + 倐)倶/2丂傛傝丄
丂丂丂丂丂丂丂丂倶 = 倛(倎 + 倐 + 倓)/(倎 + 倐)
偦偺俆丂丒丒丒丂憡帡嶰妏宍偺柺愊斾
丂丂丂丂丂丂丂仮ABC偺柺愊偼丄(倎 + 倓 + 倐)倶/2
丂丂丂丂丂丂丂嵍偺嶰妏宍偵偮偄偰丄
丂丂丂丂丂丂丂丂仮GBD佷仮ABE乮崅偝偺斾偑丄倛丗倶乯丄仮GBD偺柺愊 倎倛/2丂傛傝丄
丂丂丂丂丂丂丂仮ABE偺柺愊偼丄倎倛/2丂偺 (倶/倛)2攞
丂丂丂丂丂丂丂塃偺嶰妏宍偵偮偄偰丄
丂丂丂丂丂丂丂丂仮ICF佷仮ACE乮崅偝偺斾偑丄倛丗倶乯丄仮ICF偺柺愊 倐倛/2丂傛傝丄
丂丂丂丂丂丂丂仮ACE偺柺愊偼丄倐倛/2丂偺 (倶/倛)2攞
丂丂丂丂丂丂丂傛偭偰丄柺愊偵偍偄偰丄丂仮ABC=仮ABE+仮ACE傛傝丄
丂丂丂丂丂丂丂丂丂(倎 + 倐 + 倓)倶/2 = (倎倛/2) (倶/倛)2 + (倐倛/2) (倶/倛)2
丂丂丂丂丂丂丂埲忋偐傜丄丂倶{(倎 + 倐)倶 - 倛(倎 + 倐 + 倓)} = 0丂側偺偱丄倶 = 倛(倎 + 倐 + 倓)/(倎 + 倐)
丂丂丂丂

偦偺俇丂丒丒丒丂嶼悢
丂丂丂丂丂丂揰B丄C偐傜岝偑敪偣傜傟偨偲峫偊傞偲丄仮GBD+仮ICF=仮GBJ丂偵偍偄偰丄
丂丂丂丂丂丂朹GD偺塭偑傠偆偦偔偺挿偝AE偵側傞偺偼丄15亐(2 + 3) = 3丂側偺偱丄3 + 1攞偲側
丂丂丂丂丂丂傞偲偒偱偁傞丅丂傛偭偰丄倶亖侾亊乮俁亄侾乯亖係
丂丂丂丂丂丂丂堦斒偵丄
丂丂丂丂丂丂揰B丄C偐傜岝偑敪偣傜傟偨偲峫偊傞偲丄仮GBD+仮ICF=仮GBJ丂偵偍偄偰丄
丂丂丂丂丂丂朹GD偺塭偑傠偆偦偔偺挿偝AE偵側傞偺偼丄倓亐(倎 + 倐)丂側偺偱丄
丂丂丂丂丂丂丂倓/(倎 + 倐) + 1 = (倎 + 倐 + 倓)/(倎 + 倐)攞偲側傞偲偒偱偁傞丅
丂丂丂丂丂丂傛偭偰丄丂倶 = 倛(倎 + 倐 + 倓)/(倎 + 倐)
偦偺俈丂丒丒丒丂恾宍偲曽掱幃
丂丂丂丂丂丂揰B(0丆0)丄揰C(2+15+3丆0) = (20丆0)丂偲偡傞丅
丂丂丂丂丂丂捈慄BA 丗 倷 = (1/2)倶 丄捈慄CA 丗 倷 = (-1/3)(倶 - 20)丂側偺偱丄偦偺岎揰偼丄楢棫
丂丂丂丂丂丂曽掱幃傪夝偄偰丄(8丆4)丂丂傛偭偰丄丂倶亖係
偦偺俉丂丒丒丒丂儀僋僩儖
丂丂丂丂丂丂揰B(0丆0)丄揰C(2+15+3丆0) = (20丆0)丂偲偡傞丅
丂丂丂丂丂丂儀僋僩儖BA = s(2丆1) = (2s丆s)丄儀僋僩儖CA = (20丆0) + t(-3丆1) = (20-3t丆t)丂側
丂丂丂丂丂丂偺偱丄偦偺岎揰偼丄2s = 20-3t丄 s = t丂偺楢棫曽掱幃傪夝偔偙偲偱媮傑傞丅
丂丂丂丂丂丂(s丆t) = (8丆4)丂傛傝丄岎揰偼丄(8丆4)丂丂傛偭偰丄丂倶亖係
乮捛婰乯丂摉俫俹撉幰偺埳摗 搘偝傫偐傜暿夝傪捀偄偨丅乮暯惉俀俈擭侾侽寧侾俉擔晅偗乯
丂儘乕僜僋偺挿偝傪 倶 們倣偲偡傞偲丆嵍懁偺挿偝偼丄俀倶 們倣丄塃懁偺挿偝偼丄俁倶 們倣丂側偺偱丄
丂丂俀倶亄俁倶亖侾俆亄俀亄俁丂傛傝丄丂倶亖係乮們倣乯
乮僐儊儞僩乯丂堦斣帺慠側憡帡斾偵傛傞夝朄偑楻傟偰偄傑偟偨偹両埳摗偝傫偵姶幱偟傑偡丅