
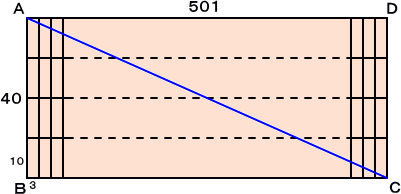
上図のような縦40m、横501mの長方形の形をした土地があり、格子状に、縦10m、
横3mの区画に分けられている。区画は全部で、668 ある。この土地の上空を、地点A
から地点Cまで飛行機が通過することになり、その迷惑料が通過する土地に支払われる
ことになった。飛行機の経路は直線で、幅がないものとする。
いったい何区画が該当するであろうか?
(答) 170区画
KSさんに解説をいただきました。(平成27年5月11日付け)
区画の長さは、本質的ではなく、1×1で考えてもよい。すると、タイルを、4×167枚敷い
たとみなせる。そうすると、公式A×Bのとき、角から角まで細く切断するとき、切断されるタ
イルの数は、A+B−(A,B) で与えられる。ただし、(A,B)はAとBの最大公約数。
問題に適用すると、4+167-1=170 を得る。
(コメント) KSさん、解説ありがとうございます。私も久しぶりに解答を考えてみました。
問題は、
0≦(4/167)x≦1、1<(4/167)x≦2、2<(4/167)x≦3、3<(4/167)x≦4
を満たす数が含まれる区間(端点が整数)の個数を求める問題なので、
0≦(4/167)x≦1から、 0≦x≦167/4=41.75 より、 42−0=42個
1<(4/167)x≦2から、 41.75<x≦83.5 より、 84−41=43個
2<(4/167)x≦3から、 83.5<x≦125.25 より、 126−83)=43個
3<(4/167)x≦4から、 125.25<x≦167 より、 167−125=42個
以上から、求める個数は、 42+43+43+42=170(個)
A+B−(A,B) は素敵な公式ですね!
KSさんから続編を頂きました。(平成27年5月12日付け)
空間のとき、小立方体を積んで、A×B×Cのおおきな直方体を作ります。角から角まで
細い針で串刺しにすると、いくつの小立方体を突き刺すか。
については、公式 A+B+C−(A,B)−(B,C)−(C,A)+(A,B,C) があります。