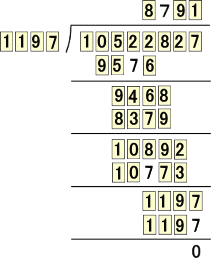
次の割り算の虫食い算もなかなかの難問である。推理の手がかりを探すのも大変である。
皆さんも、挑戦してみてはいかがですか?
(参考文献) 安福良直 著 「世界最大の虫食い算」(文春新書)
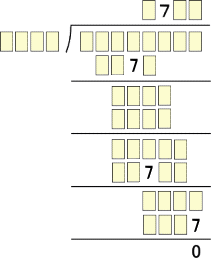
(答) ボ〜ッと眺めていると、桁数などに注意して下図のところまでは埋められる。
探究のポイントは、割る数を確定させることである。
割る数の一の位に入る可能性は、「1」、「3」、「7」、「9」の何れかが想定されるが、「8」を
「1***」に掛けて「9*7*」となるためには、「1」や「3」は起こりえない。
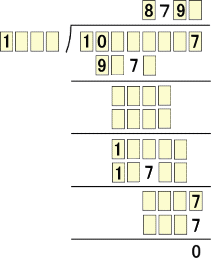
割る数の起こりえる範囲は、「1127」〜「1247」である。この中で、「8」を「1***」に掛け
て「9*7*」となる場合は、次の5通りしかない。
1147×8=9176 、1159×8=9272 、1197×8=9576 、1209×8=9672
1247×8=9976
因みに、
1147×7=8029 、1159×7=8113 、1197×7=8379 、1209×7=8463
1247×7=8729
1147×9=10323、1159×9=10431、1197×9=10773、1209×9=10881
1247×9=11223
このとき、「9」を掛けて「1*7**」となる場合は、「1197」しかないことが分かる。
この商の値「1197」が分かれば、後は機械的に順次埋められる。答えは、次の通りである。