開成高校の木部先生より伺った問題です。（平成２４年２月１１日付け）
平面上に下図のように相異なる４点Ａ、Ｂ、Ｐ、Ｑがある。ただし、Ａ、Ｂは固定された点で、
ＡＢ＝ａ とし、Ｐ、Ｑは動きうる点で線分ＡＢの同じ側にあり、ＰＡ＝ＱＢ＝ａ とする。
また、∠ＰＡＢ＜π、∠ＱＢＡ＜π とする。
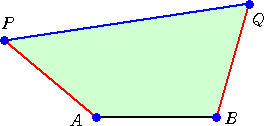
このとき、四角形ＰＡＢＱの面積の最大値を求めよ。
（答） ３
ａ2/４三角関数を用いて解いてみた。
等積変形により、ＡＢとＰＱは平行であるとしても一般性は失われない。このとき、四角形
ＰＡＢＱは線分ＡＢの垂直２等分線に関して対称な図形となる。
そこで、∠ＰＡＢ＝θとおくとき、面積が最大になるのは、π/２≦θ＜πのときである。
このとき、四角形ＰＡＢＱの面積をＳとおくと、
Ｓ＝（ａ＋ａ−ａｃｏｓθ−ａｃｏｓθ）・ａｓｉｎθ/２＝ａ2（１−ｃｏｓθ）ｓｉｎθ
なので、
Ｓ’＝ａ2（ｓｉｎ2θ−ｃｏｓ2θ＋ｃｏｓθ）＝ａ2（ｃｏｓθ−ｃｏｓ2θ）＝ａ2ｓｉｎ（3/2）θｓｉｎ（1/2）θ
π/２≦θ＜π より、 3π/4≦（3/2）θ＜（3/2）π 、π/4≦（1/2）θ＜（1/2）π
このことから、ｓｉｎ（1/2）θ＞０ で、 （3/2）θ＝π すなわち、 θ＝２π/３ のとき、
Ｓは、極大かつ最大となる。このときの最大値は、
Ｓ＝ａ2（１−ｃｏｓ（２π/３））ｓｉｎ（２π/３）＝ａ2・３/２・
/２＝３ａ2/４（※） 木部先生のお話では、上記の問題は中学１年レベルの知識で解けるとのことである。
どう解くんだろう？
興味がある方は是非挑戦してみてください。
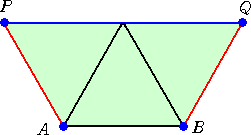
最大値を与える場合は、下図のように、正三角形が３個並ぶ場合である。正方形の場合
でないところが面白い。
空舟さんが、上記の問題を考察されました。（平成２４年２月１２日付け）
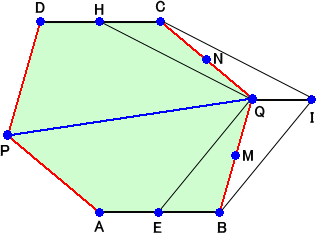
PABQを180度回転させてPQの反対(図の上)側にくっつけて、六角形ABQCDPを作る。各
辺は等しく、対辺を結ぶ四角形は平行四辺形。
AB、BQ、QC、CＤ の中点をそれぞれ E、M、N、H とする。Qを通って、ABに平行な線を引
いて、Qから六角形の外側(図で右)の向きに長さAEの点を I とする。
このとき、
四角形ABQPの面積＝六角形ABQCDPの面積/2＝五角形EBQCHの面積
ここで、四角形EBIQ、QICHは平行四辺形なので、
五角形EBQCHの面積＝三角形EHIの面積＝三角形MNIの面積×4
QM=QN=QI=ａ/2 であるから、半径一定の円に内接する三角形の面積の最大を考えるこ
とに帰着された。
もちろん、正三角形の時が最大で、求める面積は、
{3・（1/2）(ａ/2)2sin(2π/3)}×4=３
ａ2/４（＊） 正三角形の時に最大であることを示す良い手が思い浮かばない。正三角形以外の
時は等しくない２辺を等しくすることで、高さが増してより面積を大きくできることは分か
るから、「正三角形の時以外は最大ではない」ことなら言えるが...。
（コメント） なるほど、上記のように考えると、三角関数やら、微分を使わずに済みそうです
ね！円に内接する三角形で面積最大のものが正三角形であることは、中学受験
をする小学生は当然知っていますよね．．．。
空舟さんの解答が、「中学１年レベルの知識」での解答の．．．雰囲気。
らすかるさんからのコメントです。（平成２４年２月１２日付け）
円に正三角形でない△ABCが内接しているとします。また、円周の長さの1/3を ｔ とし、
弧AB=c、弧BC=a、弧CA=bとします。
ａ、ｂ、ｃ のうち t より小さいものは１個または２個です。
１個のとき、例えば、a＜t、b＞t、c≧t とします。このとき、a=c となるように頂点Bを移動
すれば、△ABCの面積は大きくなり、かつ、a、b、c のうち t より小さいものは２個になりま
す。
２個のとき、例えば、a＜t、b＜t、c＞t として、まず、a=t となるように頂点Bを移動し、aを
増やし、cを減らすと、△ABCの面積は大きくなり、その後、b=c となるように頂点Aを移動し、
bを増やし、cを減らすと、再び△ABCの面積は大きくなりますので、正三角形でない任意の
三角形は、正三角形より面積が小さいことが言えます。
空舟さんからのコメントです。（平成２４年２月１４日付け）
成程、上手いです...！四角形ABCDを考えてみたら、より簡単でした。ACを固定すれば、
BDがACに直交する直径の時に最大。そのBCを固定すれば、正方形にすると最大。
ということは、楕円に内接する四角形についても、面積は伸縮変換に対応するので、伸縮
した円に内接する正方形を元の伸縮率にした四角形が最大面積を与えるということになりま
すね。
Ｓ（Ｈ）さんが上記の問題を考察されました。（平成２４年２月１２日付け）
面積は、適当に座標をもうけ、四角形を２つに分け足すと、
S[t1,t2]=1/2*Det[{{0, 0, 1}, {a, 0, 1}, {a*Cos[t2], a*Sin[t2], 1}}]
+ 1/2*Det[{{a, 0, 1}, {a + a*Cos[t1], 0 + a*Sin[t1], 1}, {a*Cos[t2], a*Sin[t2], 1}}]
{D[ S[t1,t2],t1], D[ S[t1,t2],t2]}={0,0} を解いて、要らない解は捨てて、
S[t1, t2] /. {t1 -> Pi/3, t2 -> (2*Pi)/3}=(3*Sqrt[3]*a^2)/4 が最大値の筈。
その形は、対称性から、想定の範囲内の通りの帰結で、これ以外考えられない。
（別解） f[x, y]=(1/4*I*a^2)/E^(I*x) - 1/4*I*a^2*E^(I*x) + 1/4*I*a^2*E^(I*x - I*y)
- 1/4*I*a^2*E^(-I*x + I*y) + (1/4*I*a^2)/E^(I*y) - 1/4*I*a^2*E^(I*y)
として、 {D[f[x, y], x], D[f[x, y], y]}＝{0,0} からも得られる。
また、上記の問題で、AB=ａ、BQ=ｂ、AP=ｃ 例えば、a=5、b=7、c=3 としたらどうだろうか？
（コメント） Ｓ（Ｈ）さん、解答ありがとうございます。四角形を三角形分割し三角形の面積は
公式から、即でますね！
（追記） 当ＨＰ読者のＪ．Ｙ．さんより、中学校３年レベルでの解答をメールで頂いた。
（平成２４年２月２０日付け）
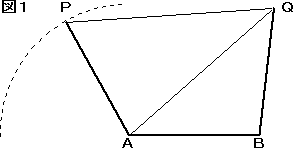
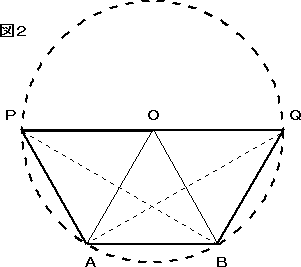一方、ＰＡ＝ＡＢ＝ＱＢ（＝ａ）より、Ａ，Ｂは