
当HPがいつもお世話になっているHN「hasu」さんからの出題です。
(平成24年2月1日付け)
正五角形のすべての対角線を引くと星形になります。(星から星の中にできる五角形を引
いたときに残る部分を葉っぱと呼ぶことにします)
一辺が1である正五角形の対角線からできる星の中にも正五角形ができ、ずっとこれを
続けられます。
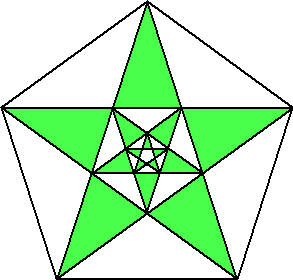
このときできるすべての星の葉っぱの部分の面積は何になるでしょうか?
上記の問題とは少し違いますが、式を一つ見つけました。
一辺が1の正n角形を考えます。すべての辺の2等分点を結ぶと、また少し小さい正n角
形ができます。
始めの正n角形を N1とし、Nkの全ての辺の2等分点を結んでできる正n角形を Nk+1 と
します。

上記の問題と同じように、Nk−Nk+1 (k:奇数)を葉っぱということにします。この葉っぱの
無限和を求めました。
葉っぱの定義より、Σ(Nr−Nr+1) (r=奇数)です。
Σ(Nr−Nr+1) (r=奇数)=Σr=1〜∞(−1)r-1Nr
一辺がkの正n角形の面積を求めます。
一辺の端の2頂点と中心を結ぶと二等辺三角形ができます。今はその半分の直角三角形
を考えます。
この三角形の小さい方の辺は、仮定より、k/2 となります。中心の角は、2π/n の半分な
のでπ/nです。
よって、正弦定理より、斜辺は、(k/2)/sin(π/n) となります。残りの辺も同様に、
{(k/2)/sin(π/n)}・cos(π/n)=(k/2)/tan(π/n)
となります。
よって、面積は、 (k/2)・(k/2)/tan(π/n)・(1/2)・(2n) = n(k/2)2/tan(π/n)
となります。
次に、Nr の一辺の長さを求めます。N1 の一辺の長さは、定義より、1です。正n角形のす
べての角の和は、公式より、(n-2)πで、一つの角の角度は、(n-2)π/n となります。
Nr の頂点は、Nr-1 の辺の二等分点なので、Nr の一辺の長さは、Nr-1 の一辺の長さを
2hとすると、2辺の長さが h で、中心の角は、(n-2)π/n であるような二等辺三角形の底
辺の長さになります。
この三角形の残りの角度を求めると、二等辺三角形より、
(π-(n-2)π/n)/2=(π-π+2π/n)/2=π/n
となるので、Nr の一辺の長さは、三角比より、2hcos(π/n) になります。
よって、 (Nr の一辺の長さ)=(Nr-1 の一辺の長さ)・cos(π/n)
という等式ができます。N1 の一辺の長さは、1なので、(Nr の一辺の長さ)=cosr-1(π/n)
となります。
今求めたいのは、Σr=1〜∞(−1)r-1Nr なので、Nr の面積を求めます。
(Nr の面積)=n({cosr-1(π/n)}/2)2/tan(π/n)
最後に、葉っぱの総和を求めると、
Σr=1〜∞(−1)r-1Nr
=Σr=1〜∞(−1)r-1・n({cosr-1(π/n)}/2)2/tan(π/n)
={n/4tan(π/n)}Σr=1〜∞(−1)r-1・cos2(r-1)(π/n)
={n/4tan(π/n)}/(1+cos2(π/n))
となります。
空舟さんからのコメントです。(平成24年2月1日付け)
一般の正多角形で、2つ隣の頂点と結ぶ対角線を引くと、同様の議論ができます。幾何的
考察によって、次のように考えられます。
(一番外の正多角形の面積) ・2tan(π/n)/tan(2π/n)
(追記) 2tan(π/n)/tan(2π/n) は 1-tan2(π/n) と書けますね。
さらに、正n角形において、「Nk−Nk+1を葉っぱ」ということですが、文脈から、奇数番目の
葉っぱだけを問題にしているようです。表記についてですが、N1等の面積はS1等の別の記
号を使った方が良いと思いました。
面積比 r = cos2(π/n) と分かった後は、以下のように考える手もあります。
すべての葉っぱだと覆いつくす、すなわち、a を1番目の葉っぱの面積として、
a(1+r+r2+...)=a/(1-r)=S1 を利用して、a(1+r2+r4+...)=a/(1-r2)=S1/(1+r) と分かります。
この考え方なら、面積比以外には、N1の面積だけを計算すれば良いことになります。
n→∞で 1/(1+r) → 1/2 となるのは、なるほどという感じですね。
ところで、「一辺が1の正n角形」よりも「半径1の円に内接する正n角形」で考えてみてはど
うでしょう。面積計算が容易にできる (n・sin(2π/n)/2) n→∞で面積が収束する。
場合によっては、複素数平面での考察が使えるかもしれない等の利点があります。