△ＡＢＣの内部に点Pがある。ＡＰ＝
、ＢＰ＝５、ＣＰ＝２、ＡＢ ： ＡＣ＝２ ： １、∠ＢＡＣ＝６０°であるとき、△ＡＢＣの面積を求めよ。
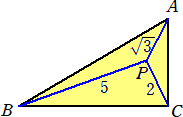
（答） ＡＣ＝ｍ とおくと、ＡＢ＝２ｍ で、余弦定理から、ＢＣ2＝ｍ2＋４ｍ2−４ｍ2・（１/２）＝３ｍ2
よって、 ＡＣ2＋ＢＣ2＝ＡＢ2 から、Ｃ＝９０°となる。
上図のように、△ＡＢＰ≡△ＡＢＱ、△ＢＣＰ≡△ＢＣＲ、△ＣＡＰ≡△ＣＡＳ となるように、３点
Ｑ、Ｒ、Ｓをとる。このとき、∠ＱＢＲ＝６０°、∠ＱＡＳ＝１２０°である。
△ＢＱＲは正三角形なので、 ＱＲ＝５
また、△ＡＱＳにおいて、余弦定理より、
ＱＳ2＝３＋３−６・（−１/２）＝９ なので、 ＱＳ＝３
したがって、 △ＱＲＳは、∠ＱＳＲ＝９０°の直角三角形となる。
よって、５角形ＡＱＢＲＳの面積は、
（
/４）・２５＋４・３・（１/２）＋（３/２）・（/２）＝７＋６となるので、求める面積は、 （７
＋６）/２ （終）以下、工事中！