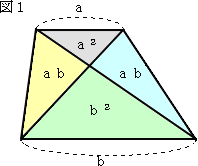
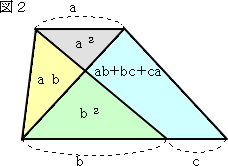
１辺の長さが１の正六角形がある。
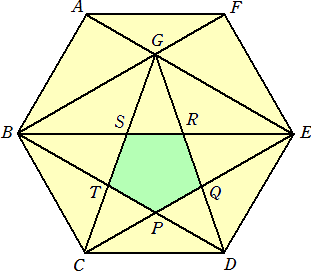
このとき、５角形ＰＱＲＳＴの面積を求めよ。
（答） ＦＮさんが初等的な解答を示されました。（平成２３年１０月１８日付け）
（解） 一辺が1の正三角形の面積をＳ、求める五角形の面積をＴとする。
Ｓ＝
/４で、Ｔ＝ΔBPE−２ΔBST だから、ΔBPEとΔBSTをＳで表せばよい。△PBE∽△PDC から、BP：PD＝２：１ なので、ΔBPE＝２/３・△DBE＝２/３・２Ｓ=(４/３)Ｓ
GSとAFの交点をC’とすると、SG：GC’＝BG：GF＝２：１ だから、GS=(２/３)C’S＝(２/３)CS
従って、GS：SC＝２：３ より、GS：GC＝２：５ なので、SR：CD＝２：５ 即ち、SR＝(２/５)CD
よって、BS＝(２CD−(２/５)CD)/２＝(４/５)CD なので、ΔBSC＝(４/５)Ｓ
また、BT：TD＝BS：CD＝４：５ より、TD＝(５/９)BD だから、ΔTCD＝(５/９)ΔBCD＝(５/９)Ｓ
従って、ΔBTC＝S−(５/９)Ｓ＝(４/９)Ｓ なので、ΔBST＝(４/５)Ｓ−(４/９)Ｓ＝(１６/４５)Ｓ
このとき、 Ｔ＝ΔBPE−２ΔBST＝(４/３)Ｓ−２・(１６/４５)Ｓ＝(２８/４５)Ｓ より、
Ｓ＝
/４ を代入して、 Ｔ＝２８/４５・/４＝(７/４５) （終）らすかるさんが、別解を示されました。（平成２３年１０月１８日付け）
（解） 1辺が1の正三角形の面積をS、高さをhとします。AF：BE＝１：２ から、△GSRの高さ
は、(２/３)h で、△GCDの高さは、(５/３)h となる。
よって、△GCD＝(５/３)Ｓ で、△GSR＝(２/５)2△GCD＝(４/１５)Ｓ
このとき、台形SCDR＝(５/３)Ｓ−(４/１５)Ｓ＝(７/５)Ｓ
また、SR＝２/５ なので、BS＝(２−２/５)/２＝４/５ となり、BS：CD＝４：５
よって、△TCDの高さは、(５/９)h で、△PCDの高さは、(１/３)h
以上から、求める面積は、
(７/５)Ｓ−２・(５/９)S＋(１/３)Ｓ＝(２８/４５)Ｓ＝(７/４５)
（終）（コメント） ＦＮさん、らすかるさん、解答ありがとうございます。
最初座標幾何で計算したのですが、計算ミスがあったようです！お詫びします．．．ｆ(^^;)。
再度計算し直してみました。
ＢＥを ｘ 軸とし、点Ｂを座標軸の原点とする。このとき、直線ＢＦは、ｙ＝(１/
)ｘ で、直線ＡＥは、ｙ＝(−１/
)(ｘ−２) より、交点Ｇの座標は、（１，１/）同様にして、点Ｐの座標は、（１，−１/
）また、Ｃ（１/２，−
/２） 、Ｄ（３/２，−/２） なので、直線ＣＧの方程式は、 ｙ＝(５
/３)(ｘ−１/２)−/２＝(５/３)ｘ−４/３このとき、点Ｓの座標は、（４/５，０） で、対称性から、点Ｒの座標は、（６/５，０）
直線ＢＰの方程式は、 ｙ＝−(１/
)ｘよって、直線ＣＧと直線ＢＰの交点Ｔの座標は、（２/３，−２
/９）さらに、対称性から、点Ｑの座標は、（４/３，−２
/９）このとき、 △ＰＳＲ＝(２/５)(１/
)/２＝/１５また、ベクトルＳＰ＝（１/５，−１/
）、ベクトルＳＴ＝（−２/１５，−２/９）より、△ＰＴＳ＝(１/２)｜(１/５)(−２
/９)−(−１/)(−２/１５)｜＝２/４５以上から、５角形ＰＱＲＳＴの面積は、
△ＰＳＲ＋２△ＰＴＳ＝
/１５＋４/４５＝７/４５（検証の結果、△ＰＴＳを２倍するのを忘れていたようです．．．ｆ(^^;)。）
当ＨＰ読者のＪ．Ｙ．さんが上記の問題を考察されました。（平成２３年１２月２３日付け）
解答を、中学３年でも納得できるように説明してみました。まず、公式を２つ理解して下さ
い。
公式１（中３で学習）
