正方形ＡＢＣＤにおいて、ＢＣ、ＣＤの中点をそれぞれＭ、Ｎとおく。線分ＭＤと線分ＮＡの交
点をＰとする。
△ＤＰＮの面積が ５ のとき、△ＡＭＰの面積を求めよ。
（答） ＤＮ＝ａ とおくと、ＡＤ＝２ａ 、ＡＮ＝
ａ となる。また、ＡＮ⊥ＭＤ で、直角三角形ＡＤＮ∽直角三角形ＤＰＮ より、
ＤＰ＝２ａ/
、ＰＮ＝ａ/よって、 直角三角形ＤＰＮの面積は、 （１/２）・（２ａ/
）・（ａ/）＝ａ2/５＝５ より、ａ＝５ となる。このことから、正方形ＡＢＣＤの１辺の長さは、１０で、面積は、１００となる。
△ＡＢＭ＝△ＤＣＭ＝△ＡＤＮ＝２５ なので、
△ＡＭＰ＝正方形ＡＢＣＤ−（△ＡＢＭ＋△ＤＣＭ＋△ＡＤＮ−△ＤＰＮ）
＝１００−（２５＋２５＋２５−５）＝３０ （終）
（コメント） 上記の計算の副産物として、 ＤＰ ： ＰＭ＝２ ： ３ であることが分かる。
また、 ＤＰ ： ＰＭ＝２ａ/
： （ａ−２ａ/）＝２ ： ３ としてもよい。よおすけさんからのコメントです。（令和６年６月２日付け）
別の視点で興味があったのですが、△ＡＰＤの面積は、△ＤＰＮの面積の４倍でしょうか？
（コメント） △ＡＭＰ＝３０ で、ＤＰ ： ＰＭ＝２ ： ３ から、△ＡＰＤ＝２０ となる。
よって、△ＤＰＮ＝５ より、 △ＡＰＤ＝４△ＤＰＮ
よおすけさんの予想通り、４倍になりますね。
よおすけさんからのコメントです。（令和６年６月４日付け）
ありがとうございます。実は、下図で以下のようにやっていました。
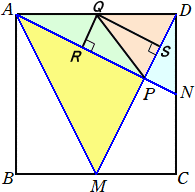
△APDで、辺DAの中点をQとし、QからPに線を引くと、△QAP＝△QPD である。
△QAPでQから辺APへ垂線を引き、その交点をR、△QPDでQから辺PDへ垂線を引き、そ
の交点をSとすると、
△QAR＝△QPR 、△QPS＝△QDS
である。△QAP＝△QPD なので、 △QAR＝△QPR＝△QPS＝△QDS
上記が正しいか判らなかった上、△QAR、△QPR、△QPS、△QDSの面積が何れも△DPN
と同じ 5 でいいのかも判らなかったため、前回は、ためらっていました。
（コメント） なるほど、幾何的に示す方法があるんですね！
Ｑは辺ＡＤの中点なので、△QAP＝△QPD である。
∠ＡＰＤ＝９０°で、ＱＲ
ＤＰ から、中点連結定理より、ＲはＡＰの中点となる。よって、 △QAR＝△QPR である。
同様にして、ＱＳ
ＡＰ から、Ｓは辺ＰＤの中点となる。よって、 △QPS＝△QDS である。
すなわち、 △QAP＝△QPD から、 △QAR＝△QPR＝△QPS＝△QDS
一方、 △QDS≡△ＤＮＰ より、 △QDS＝△ＤＮＰ
以上から、△ＡＰＤ＝４△QDS＝４△ＤＮＰ となり、△ＡＰＤの面積は、△ＤＰＮの面積の４倍
となる。
＃△ＡＰＤは∠ＡＰＤ＝９０°の直角三角形なので、点Ｑは、３点Ａ、Ｐ、Ｄを通る円の中心と
なるので、 ＱＡ＝ＱＰ＝ＱＤ が成り立つ。
よって、△ＱＡＰ、△ＱＰＤは２等辺三角形となることが分かる。
よおすけさんからのコメントです。（令和６年６月１１日付け）
また、別の視点で考えてみました。
△ＡＭＰの面積が３０ということなので、△ＤＰＮ ６個と同じ面積になる...はずですが、与えら
れた図の枠内では、△ＤＰＮ ４個が詰められた四角形ＰＭＣＮや△ＡＰＤとは異なり、△ＡＭＰ
の枠内では、△ＤＰＮ ６個が詰められなかったので、下図のように、辺ＡＰ側を変形しました。
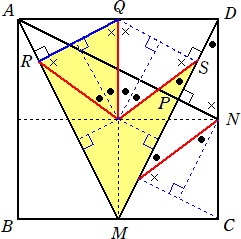
この黄色の部分で示した多角形の面積も、△ＡＭＰの面積と同じ３０です。
（コメント） 合同による等積変形により、黄色の部分の多角形は、△ＡＭＰそのものに変形
することができる。（下図参照）
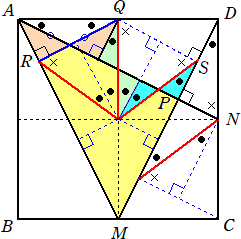
＃点Ｓが線分ＤＰの中点になるところが面白いですね！
DD++ さんからのコメントです。（令和６年６月７日付け）
問題では正方形になっていますが、実は長方形という条件でも解くことができます。
ポイントは、AB と DM を左下方向に延長して交点を作ること。
＃愛知県公立高校入試は、なぜか図形問題がやたら難しく、この長方形の外にはみ出す
補助線の引き方がかなりの頻度で出題されます。他の都道府県ではどうなんでしょう？
（コメント） DD++ さんから、「長方形という条件でも解くことができる」とのご教示を得て、計
算してみた。
この場合、△ＤＰＮは直角三角形ではなくなるので、別途の方策が必要である。DD++ さん
のヒントから、直線ＤＭと直線ＡＢの交点をＥとおくと、
