当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（令和６年２月１７日付け）
（１） 下図のように直角三角形ABCにACを１辺とする正方形とBCを１辺とする正方形をか
き、２つの点D、Eを直線で結びます。このとき、三角形CDEの面積は何cm2ですか。
（２） 下図のように直角三角形ABCと、AD、BD、CDをそれぞれ１辺とする正方形があります。
このとき、CDを１辺とする正方形の面積は何cm2ですか。
（３） AB=AD、AD：DC＝２：３、∠A＝150°、∠D＝90°である四角形ABCDがあります。辺
BCをのばしたところに２つの点E、Fをとります。次に、直角三角形AEGと直角三角形DFH
をかいたところ、下図のようになりました。直線ADと直線GHが平行のとき、三角形ABEは
三角形DCFの面積の何倍ですか。
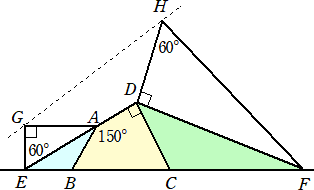
（出典） 渋谷教育学園幕張中学校（２０２０）問題4
（答）（１） △ＣＤＥ＝△ＡＢＣ＝８×４×（１/２）×（１/２）＝８（ｃｍ2）
（２） ＣＤ2＝２2−１2＝３（ｃｍ2）
（３） △ＡＢＥ＝（１/２）・ＡＢ・ＡＥ・ｓｉｎ∠ＢＡＥ
△ＡＤＧ＝（１/２）・ＡＤ・ＡＧ・ｓｉｎ（１８０°−∠ＢＡＥ）＝（１/２）・ＡＢ・ＡＧ・ｓｉｎ∠ＢＡＥ
なので、 △ＡＢＥ/△ＡＤＧ＝ＡＥ/ＡＧ＝２/
である。また、直線ADと直線GHが平行なので、 △ＡＤＧ＝△ＡＤＨ
ここで、△ＡＤＨ＝（１/２）・ＡＤ・ＤＨ・ｓｉｎ∠ＡＤＨ
△ＤＣＦ＝（１/２）・ＤＣ・ＤＦ・ｓｉｎ（１８０°−∠ＡＤＨ）＝（１/２）・ＤＣ・ＤＦ・ｓｉｎ∠ＡＤＨ
なので、 △ＡＤＨ/△ＤＣＦ＝（ＡＤ・ＤＨ）/（ＤＣ・ＤＦ）＝（１/
）・（２/３）よって、
△ＡＢＥ＝（２/
）△ＡＤＧ＝（２/）△ＡＤＨ＝（２/）・（１/）・（２/３）△ＤＣＦ＝（４/９）△ＤＣＦ
以上から、三角形ABEは、三角形DCFの面積の４/９倍である。 （終）
（コメント） 上記では、三角比を用いたが、初等的な解法はあるのだろうか？
よおすけさんから、（２）の別解をいただきました。（令和６年２月１９日付け）
（別解）
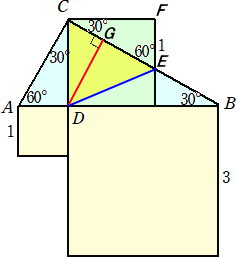
上図において、△ＡＤＣ≡△ＥＦＣ より、ＣＥ＝２ である。また、△ＡＢＣ∽△ＤＢＧ より、
ＡＢ ： ＤＢ＝ＡＣ ： ＤＧ なので、 ４：３＝２：ＤＧ すなわち、 ＤＧ＝３/２ となる。
ＣＤを１辺とする正方形の面積は、その正方形の内部にある底辺が２cm、高さが（３/２）cm
の三角形の面積の２倍に等しいので、 ２×（３/２）÷２×２＝３（ｃｍ2） （終）
以下、工事中！