次の問題は、発想がとても面白い問題である。
直径の両端を Ａ、Ｂとする半径１の半円Ｏがある。半円の弧ＡＢ上を点Ａより点Ｂまで点Ｐ
が移動する。
さらに、線分ＡＰに関して中心Ｏの反対側に、△ＡＰＱが正三角形になるように点Ｑを取る。
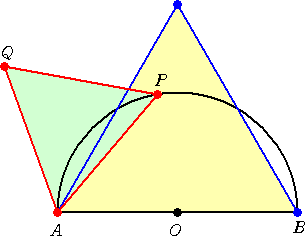
このとき、線分ＡＱが通過する領域の面積を求めよ。
（答） この問題を、次のように解いてしまったら大人げないだろう。
ＡＢを始線、Ａを極とする極座標で考える。
点Ｑ（ ｒ ，θ ）とすると、点Ｐ（ ｒ ，θ−π/３ ）なので、
ｒ＝２ｃｏｓ（θ−π/３） 、 π/３≦θ≦π/２＋π/３
このとき、求める面積 Ｓ は、
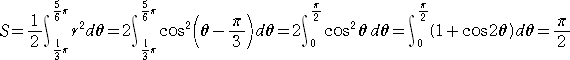
である。
実は、求める面積は、半円Ｏの面積に等しい。このことに気がつけば、積分を用いなく
ても答えは暗算で求められることだろう。
このことは、当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんも指摘されている。
（平成２２年１１月２７日付け）
ＡＢを直径とする半円(内部を含む)をＳとし、線分ＡＱ全体がつくる図形をＴとすれば、
ＴはＳをＡのまわりに６０°回転した図形である。・・・・・(＊)
従って、Ｔの面積はＳの面積と同じで、π/２である。
(＊)は証明すべきかもしれませんが、ほとんど明らかとも言えます。
（コメント） ＦＮさん、ありがとうございます。
上記の（＊）については、証明を考えました。
ｒ＝２ｃｏｓ（θ−π/３）＝ｃｏｓθ＋
ｓｉｎθ よりｒ2＝ｒ・ｃｏｓθ＋
ｒ・ｓｉｎθ すなわち、 ｘ2＋ｙ2＝ｘ＋ｙよって、 （ｘ−１/２）2＋（ｙ−
/２）2＝１ より、点Ｑは、中心（１/２ ，/２）、半径１の半円上を動くことが分かる。
（コメント） 上記の（＊）の証明ですが、ここはもっと軽妙に、
２点Ｐ、Ｑは常に、ＡＰ＝ＡＱ、 ∠ＰＡＱ＝６０°である。よって、点Ｑの描く軌跡は
点Ｐの描く軌跡と合同である
ことからも察することが出来ると思います。