下図のように、直角２等辺三角形ＡＢＣの内部に点Ｐをとり、
ＰＢ＝ＰＣ＝８ 、 ∠ＡＢＰ＝∠ＡＣＰ＝２２．５°（＝θとおく）
とする。
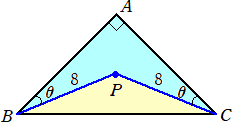
このとき、四角形ＡＢＰＣの面積を求めよ。
（答） ∠ＢＰＣ＝１３５°なので、 ＢＣ2＝８2＋８2−２・８2・ｃｏｓ１３５°＝６４（２＋
）よって、 ＢＣ＝８√（２＋
） で、ＡＢ＝ＡＣ＝４√（４＋２）ゆえに、 △ＡＢＣ＝４√（４＋２
）・４√（４＋２）/２＝３２＋１６また、△ＰＢＣ＝８・８・ｓｉｎ１３５°・（１/２）＝１６
なので、四角形ＡＢＰＣの面積は、 ３２＋１６
−１６＝３２ （終）この問題については、次のような初等的な解法が知られている。
（別解） 与えられた図形を４枚組み合わせて、下図を得る。
下図のように、補助線を引いて考える。
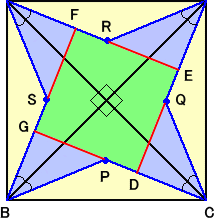
このとき、１辺の長さが８の正方形ＤＥＦＧの周りに、４つの直角２等辺三角形（△ＢＰＧ等）
が出来る。
４つの直角２等辺三角形の面積の和は、 ８・８/２・２＝６４ なので、
４×四角形ＡＢＰＣ＝６４＋６４＝１２８ から、 四角形ＡＢＰＣ＝３２ （終）
（コメント） この問題は、三角比を用いれば何でもないですが、上記のように工夫すると、
簡単な計算で求められます。このアイデアには脱帽です。