長方形の面積　　 　　　 　　　　 　　　　 　　　　　　　　　　　　　　　

　長方形ＡＢＣＤにおいて対角線ＡＣ上に点Ｐを、ＰＡ＝８、ＰＢ＝７、ＰＣ＝２　となるように取
る。このとき、長方形ＡＢＣＤの面積を求めよ。

　　　
































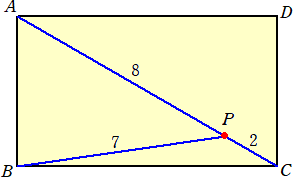
（答）　２５

　実際に、対角線の交点をＯとし、∠ＢＯＰ＝θとおく。

　　　

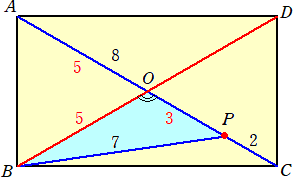
　余弦定理から、

　　　ｃｏｓθ＝（９＋２５−４９）/３０＝−１/２　なので、　θ＝１２０°

　　よって、長方形ＡＢＣＤの面積は、　１０×１０×ｓｉｎ１２０°×（１/２）＝２５


（コメント）　名古屋大学（１９６３）の伝説の図形問題：

　　正方形ＡＢＣＤ内の点Ｐに対して、ＰＡ＝７、ＰＢ＝５、ＰＣ＝１のとき、正方形の面積
　を求めよ。

を意識して問題を作ろうとしたが、陳腐な問題になってしまった。７、５、１という数字の配列
は絶妙ですね！


　moonlightさんからのコメントです。（令和２年８月２４日付け）

　その元になった名大の問題が面白かったので、少し調べてみると、

　正方形ABCD内の点Pに対して、PA＝８、PB＝６、PC＝３ のとき、正方形の面積を求めよ。

としても問題が成立することが分かりました。

　多分他にも沢山あると思うのですが如何でしょう。


　DD++さんからのコメントです。（令和２年８月２４日付け）

　その場合、ＰＤ＝√３７≠６ になるので、同じ解き方は成立しないような．．．。


（コメント）　Ｐから辺ＡＤに平行線を引き、辺ＡＢとの交点をＥ、辺ＣＤとの交点をＦとする。

　　ＡＥ＝ａ、ＥＢ＝ｂ　とおく。

　同様に、Ｐから辺ＡＢに平行線を引き、辺ＢＣとの交点をＧ、辺ＡＤとの交点をＨとする。

　　ＡＨ＝ｐ、ＨＤ＝ｑ　とおく。ＰＤ＝ｘ　とおく。

　このとき、　ａ²＋ｐ²＝６４　、ｂ²＋ｐ²＝３６　、ｂ²＋ｑ²＝９　、ａ²＋ｑ²＝ｘ²　なので、

　ｐ²−ｑ²＝２７　、　ｐ²−ｑ²＝６４−ｘ²　より、　２７＝６４−ｘ²　すなわち、　ｘ²＝３７

　よって、　ＰＤ＝√３７

　これだと、ＡＣは正方形の対角線となり得ないので、問題は難しくなりますね！

　面積だけを求めるんだったら次のようにすればいいのかな？

　正方形の一辺の長さをａとおくと、

　∠ＰＢＣ＝θとおくと、　ｃｏｓθ＝（ａ²＋２７）/１２ａ

　　ｓｉｎθ＝ｃｏｓ（９０°−θ）＝（ａ²−２８）/１２ａ

　よって、　（ａ²＋２７）²＋（ａ²−２８）²＝１４４ａ²　より、　２ａ⁴−１４６ａ²＋１５１３＝０

　θは鋭角なので、　ａ²＞２８　なので、　ａ²＝（７３＋√２３０３）/２

　よって、正方形の面積は、　（７３＋√２３０３）/２（≒６０．４９４７９１１）


（コメント）　ＰＤ＝√３７≒６　で、折れ線ＡＰＣはほぼ対角線であると考えると、

　その対角線の長さは、ほぼ１１で、正方形の一辺の長さは、ほぼ１１/√２

　よって、正方形の面積は、ほぼ１２１/２＝６０．５　となり、上記で計算したものとほとんど
一致している。


　よおすけさんからのコメントです。（令和２年８月２６日付け）

　冒頭の問題を

　長方形ＡＢＣＤにおいて対角線ＡＣ上に点Ｐを、ＰＡ＝7、ＰＢ＝5、ＰＣ＝1　となるように取る。

とした場合、cos∠BOP=0、sin∠BOP=1、∠BOP=∠Rとなり、長方形ＡＢＣＤの面積は正の整
数になる。（ただし、Ｏは対角線の交点）