
台形ABCDにおいて、対角線BD上に点EをAD‖ECとなるようにとり、CEの延長と辺AB
との交点をFとおく。このとき、△AEDの面積Sと△BCEの面積Tをそれぞれ求めよ。
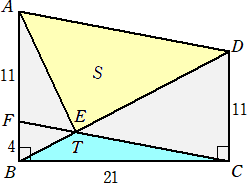
(答) Sは、平行四辺形AFCDの面積の半分なので、S=11×21÷2=231/2
また、△ABE=△ABD−S=15×21÷2−11×21÷2=42
よって、 BE:ED=42:231/2=4:11 なので、
T=△BCD×(4/15)=21×11÷2×(4/15)=154/5
(コメント) 上記の計算で、BE:ED=4:11 を示すのに、△ABEを利用したが、直接的に
次のようにしても求められる。
△FBEと△CDEは相似なので、BE:ED=FB:CD=4:11