面積計算10　 　　 　　　 　　　　 　　　　 　　　　　　　　　　　　　　　

　黄金比に関わる面積計算の問題です。

問題１　平行四辺形ABCDにおいて、ＡＢ＝ａ、ＢＣ＝ｂ　とする。点Ｅを辺ＡＤの黄金分割点
　　　　　とする。直線ＢＥと直線ＣＤの交点をＦとすると、△ＡＢＥ＝△FECが成り立つことを
　　　　　示せ。


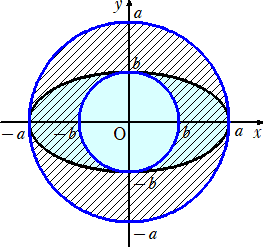
問題２　楕円　ｘ²/ａ²＋ｙ²/ｂ²＝１　の面積と半径ａ、ｂ（ａ＞ｂ）の円環面の面積が等しいと
　　　　　き、　ａ/ｂ＝（１＋）/２　（黄金比）　となることを示せ。

　　　　


























（答）　問題１の解

　ｘ ： ｂ−ｘ＝ｂ ： ｘ　とおくと、　ｘ＝（−１）ｂ/２　である。

　△ＡＢＥ＝（−１）ａｂｓｉｎθ/４　　（θ＝∠ＢＡＤ）

　ｘ ： ａ＝ｂ−ｘ ： ＤＦ　より、　ｘ・ＤＦ＝ａｂｰａｘ＝（３−）ａｂ　なので、

　ＤＦ＝（−１）ａ/２　、ＥＤ＝ｂ−ｘ＝（３−）ｂ/２

　よって、

△ＦＥＣ＝｛（３−）ｂ/２｝｛−１｝ａ/２｝（１/２）ｓｉｎθ＋｛（３−）ｂ/２｝｛ａ｝（１/２）ｓｉｎθ

　　　　＝（√５−１）ａｂｓｉｎθ/４

　以上から、△ＡＢＥ＝△FECが成り立つ。


問題２の解

　楕円　ｘ²/ａ²＋ｙ²/ｂ²＝１　の面積は、　πａｂ

　　半径ａ、ｂ（ａ＞ｂ）の円環面の面積は、π（ａ²−ｂ²）

　題意より、　ａ²−ｂ²＝ａｂ　すなわち、　ａ²−ａｂ−ｂ²＝０　より、　（ａ/ｂ）²−ａ/ｂ−１＝０

　よって、　ａ/ｂ＝（１＋）/２