
円 x2+y2=1 外の1点A(−2,0)から円と2点P、Qで交わる直線を引く。
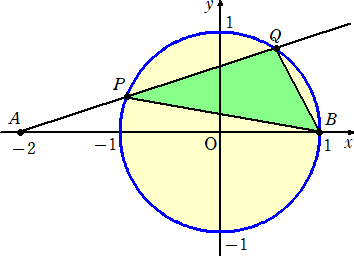
このとき、点B(1,0)を頂点とする△PBQの面積の最大値を求めよ。
(出典:青山学院大学理工学部(1989年))
(答) 線分PQの中点をMとおくと、PQ⊥OMである。そこで、∠POM=θとおくと、
PQ=2sinθ (0<θ<π/2)
このとき、 OM=cosθ で、△PBQのPQを底辺とする高さは、(3/2)cosθ
よって、△PBQ=2sinθ・(3/2)cosθ・(1/2)=(3/4)sin2θ
0<2θ<π より、 θ=π/4のとき、Sは最大値3/4をとる。 (終)
(コメント) この問題で、点Aを通る直線の方程式を、y=m(x+2) として解こうとすると、
膨大な計算の嵐が待っている。ここは、軽妙に上記のように解くのがエレガントだ
ろう。
らすかるさんから別解をいただきました。(令和元年6月14日付け)
(別解) AO:AB=2:3 から、△PBQ=(3/2)△POQ なので、
△PBQが最大 ⇔ △POQが最大
△POQは、OPが底辺と考えると、高さが最大になるのは、∠POQが直
角のときで、高さ=1
よって、△POQの面積は、最大 1/2 なので、△PBQの面積の最大値は、
(1/2)(3/2)=3/4 (終)
(コメント) なるほど!三角関数を出すまでもなかったわけですね...。
S(H)さんからのコメントです。(令和元年6月14日付け)
面積は、 3*Abs[(m*Sqrt[1-3*m^2])/(1 + m^2)] で、膨大[な計算の嵐]とまでは云い難い。
m =1/Sqrt[7]のとき、最大値 3/4 である。
(コメント) 上記のS(H)さんからのコメントに背中を押されて、実際に計算してみた。
点P(−2,0)を通る直線の方程式を、y=m(x+2) とおく。
円 x2+y2=1 と連立して整理すると、 (1+m2)x2+4m2x+4m2−1=0
P(α,m(α+2))、Q(β,m(β+2))とすると、
α+β=−4m2/(1+m2) 、αβ=(4m2−1)/(1+m2) から、
PQ2=(1+m2)(α−β)2=4(1−3m2)/(1+m2)
また、点Q(1,0)と直線 y=m(x+2) との距離hは、 h2=9m2/(1+m2)
よって、△PBQの面積をSとおくと、
S2=9m2(1−3m2)/(1+m2)2
ここで、m2=t とおくと、0<t<1/3 で、 y=t(1−3t)/(1+t)2 とおくと、
y’=(1−7t)/(1+t)2 から、t=1/7 で、yは極大かつ最大となる。
よって、yの最大値は、y=1/16 なので、△PBQの面積の最大値は、3/4 (終)
(コメント) 確かに、計算の嵐とまではいかないまでも結構ハードな計算でした。