
正方形ABCDの内部に点Eがあり、Eで垂直に交わる直線がABとADと交わる点をそれ
ぞれP、Qとおく。
EP=EQ で、AP+AQ=5のとき、四角形APEQの面積を求めよ。
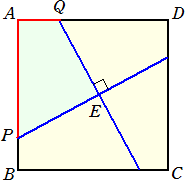
(答) AP=x とおくと、AQ=5−x で、 PQ2=x2+(5−x)2
このとき、 EP=EQ=PQ/√2 で、
四角形APEQの面積=x(5−x)/2+(x2+(5−x)2)/4=(x+5−x)2/4=25/4
(コメント) 上記の解答では、文字を用いて求めているが、全然小学生的でない。次のよう
に考えると楽に求められそうだ。
(別解) 四角形APEQを4枚用意し、順次反時計回り(または時計回り)に貼り合わせると、
1辺の長さが5の正方形ができる。よって、求める面積は、 25÷4=25/4 (終)
(コメント) (別解)のように文字を使わない解法もエレガントであるが、文字を使って、奇麗
に、その文字が消失するという解法も素敵に感じる。
カルピスさんからのコメントです。(令和元年6月6日付け)
四角形APEQを90度づつ回転させていくと、一辺が5の正方形ができる。
では、この正方形を構成している4ピースを並べ替えて、真ん中に小さな正方形(一辺が
APとAQとの【差】になる)を組み入れて、新たな正方形をつくるには?
(コメント) 真ん中の小さな正方形の頂点にすべてAがくるように配置すれば、やはり、正方
形(一辺がPEとQEとの【和】になる)が出来ますね!
以下、工事中!