
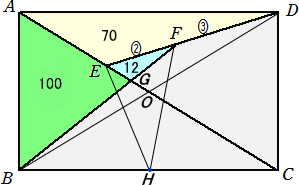
長方形ABCDにおいて、AC上に点Eをとり、線分EDを2:3に内分する点をF、BFとACの
交点をGとする。このとき、△AED=70、△EFG=12、△ABG=100である。
次の問いに答えよ。
(1) 長方形ABCDの面積を求めよ。
(2) 辺BCの中点をHとするとき、△EHFの面積を求めよ。
(答) (1) △FGD=18 より、△EGD=30 なので、 AE:EG=70:30=7:3
よって、△EBG=100×3/10=30 より、 △EBF=42
これより、 △FBD=42×3/2=63 なので、
長方形ABCD=2×(100+70+12+63)=490
(2) △EBC=△EBG+△GBC=30+(245−100)=175 なので、△EBH=175/2
また、△DHC=245/2 なので、△EHF=S とおくと、
長方形ABCD=△ABE+△EBH+△AED+S+(3/2)S+△DHC
より、 70+175/2+70+(5/2)S+245/2=490 なので、 S=56
らすかるさんから別解をいただきました。(令和元年5月24日付け)

(1) Fを通りACに平行な直線とBDの交点をPとすると、BO:OP:PD=5:2:3 なので、
EO:FP=5:3、FP:GO=7:5 から、EO:GO=7:3 すなわち、EG:GO=4:3
AG:AE=△ABG:△ADE=10:7 なので、AE:EG=7:3
従って、AE:EG:GO=28:12:9 から、AE:AO=4:7 なので、
求める面積は、70×(7/4)×4=490
(1)(別解の別解です)
メネラウスの定理により、△DEOで、EG/GO=(EF/FD)(DB/BO)=4/3
AG:AE=△ABG:△ADE=10:7 なので、AE:EG=7:3
従って、AE:EG:GO=28:12:9 から、AE:AO=4:7 なので、
求める面積は、70×(7/4)×4=490
(2) HDとACの交点をQとすると、AQ:QC=2:1 となることから(※)、EQ:AQ=4:7
よって、 △EHF=(2/5)△EHD=(2/5)(4/7)△AHD=(2/5)(4/7)(1/2)(長方形ABCD)=56
(※)Qが△BCDの重心であることからただちにわかります。