面積迷路 　　 　　 　　　 　　　　 　　　　 　　　　　　　　　　　　　　　

　数学セミナー　’１６　１２月号（日本評論社）にパズル作家の稲葉直貴さんが作られた「面
積迷路」の問題に興味を持ち、類題を作ってみました。（平成２８年１２月２２日付け）

　小学校低学年の算数教育用として考案されたそうで、いかに工夫して整数の範囲で問題
を解くかが知恵の出しどころです。

　下図の黄色い部分の面積は如何？ただし、図は必ずしも正確に描かれていませんが、何
れも長方形の集まりです。

　（１）は平易ですが、（２）（３）とだんだん難しくなっていきます。

（１）	（２）
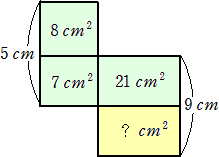（３）

（答）　（１）　６０ｃｍ²　　（２）　３ｃｍ²　　（３）　３６ｃｍ²


　よおすけさんからのコメントです。（平成２８年１２月２３日付け）

（１）の解：　四角形の8cm²、7cm²を合わせると15cm²で、一辺の長さが5cmなので、もう一

辺の長さは、15÷5=3cm

　四角形の21cm²は、7cm²の3倍なので、一辺の長さは、3の2乗の9cm。21cm²、？cm²を

合わせると、9×9=81cm²で、黄色い部分は、81-21=60cm²


（コメント）　よおすけさん、正解です。


　りらひいさんからのコメントです。（平成２８年１２月２３日付け）

　ものすごくどうでもいいかもしれませんが、ちょっと気になったので投稿してみます。

　「一辺の長さは、3の2乗の9cm。」という書き方について。

　数値計算を進めていく上では確かに「3の2乗」と同じ計算なのですが、実際には、「3cmの
3倍が9cm」なのであって、（長さ次元の量）×（比の値[無次元数]）＝（長さ次元の量）　とい
う式構成となっています。「3の2乗」という表記にわずかながら違和感を感じるのは、わたし
が物理系の人間だからでしょうか。途中式とみれば間違ったことを言っているわけではない
ので、そこまで気にするような話でもないのですけど。みなさんはどうですか？

（そもそも累乗を習っていないということを置いておいても、小学生はこんなことは考えない気
もしますが！）


　らすかるさんからのコメントです。（平成２８年１２月２３日付け）

　私も違和感を感じていました。3cmの3倍なので、3×3と書かないと気持ち悪いです。

# 「飴4粒入りの小袋が3袋入っている箱が2箱セットで売られているとき、1セットの中に飴は
　何個か」という問題で、4!=24個と答えるのと同じような気持ち悪さです。


　よおすけさんからのコメントです。（平成２８年１２月２３日付け）

　当初は、「一辺の長さは、3の2乗の9cm。」の部分は、「3の3倍」と書いていましたが、「これ
でいいのだろうか」と思って悩んでしまい、「3の2乗」に書き換えました。昨日の朝に、初めて
問題を見たときは、与えられた辺の長さが2ヶ所しかなくて意味が分からず、解法が思いつく
まで1日かかりました。


　カルピスさんからのコメントです。（平成２８年１２月２３日付け）

　三輪みわ　著　「面積パズル」　（日本文芸社）　にも同様の問題が載っています。

　　　（コメント）　表紙の問題の解：　左上は、９ｃｍ、右下は、３８ｃｍ²　かな？問題レベルと
　　　　　　　　　しては、このページの問題（１）程度でしょう、多分。

　問題（１）〜（３）の全て解けますけど、（２）（３）は「分数」を使ってしまいました。本来なら
「整数」だけを使って、迷路を辿っていき「面積」を求めるというのが「面積迷路」だと思って
いたので、私の解き方の知恵が足りなかったのでしょうか？

　上記の本は、確か「整数だけ」で解ける問題だったと思います。何年も前のことなので、
記憶が、あやふやですが・・・・・。作者によって異なるのかな？稲葉さんと三輪さんとでは。

　作者・三輪さんの「面積迷路」は「分数を使わない・整数だけを使って求める」なので、私は、
「整数」だけを使って面積を求めるというのが、本来の「面積迷路」というパズルの姿だと思っ
ていたのですが・・・・・。ルールがハッキリと分からないので、何とも言えませんが・・・・・。


　らすかるさんからのコメントです。（平成２８年１２月２３日付け）

　整数だけで解けますね。

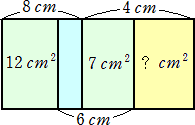
（２）　8cmを2cmと6cmに分ければ、6cmの下は、7cm²+空白部分になるから、2cmの下は
　　5cm²。よって、4cmでは10cm²だから、黄色の部分は、10-7=3cm²

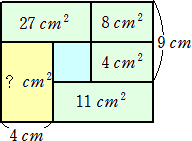
（３）　8cm²を水平線で上下二つに分ければ4cm²が二つになって、9cmが3cmずつ、つまり、
　　8cm²の縦が6cm、4cm²の縦が3cm。?cm²の四角形の右側の辺を上に伸ばして27cm²
　　を二つに分けると、左側が4cm×6cm=24cm²になるから、右側は、3cm²。
　　　従って、その3cm²と8cm²を合わせると下の11cm²と同じになるから、下の11cm²も高
　　さは6cm。
　　　よって、?cm²の四角形の高さは、3+6=9cmだから、面積は、4×9=36cm²


（コメント）　らすかるさん、（２）（３）ともに正解です。黄色部分の長方形の高さが実は「９ｃｍ」
　　　　　　ということをアクロバット的に導く（３）が一番好きで魅了されます！２２日午後出張
　　　　　　で電車に乗っている間、ずっとこの問題をいじっていてようやく完成しました。


　カルピスさんからのコメントです。（平成２８年１２月２３日付け）

　大変失礼いたしました。よく読んだら、「整数」だけを使ってと書いてありましたね。らすかる
さん　有難うございます。自分の間違いに気づき、急いで投稿しましたが、既に遅かりし・・・。
（らすかるさんと同じ１４時４１分台に投稿．．．。）


　よおすけさんからのコメントです。（平成２８年１２月２４日付け）

（２）　まず、以下は言えるかと思われます。

　7cm²＋？cm²は、12cm²＋空白の半分で、7cm²＋空白と12cm²＋？cm²は等しい。「整

数の範囲で」ということなので、？も整数として、上の2つが両方あてはまるまで書きます。

　？＝0cm²のとき、空白は2cm²。このとき、7cm²＋空白は12cm²＋？cm²より小さいので、
？は0ではない。

　？＝1cm²のとき、空白は4cm²。7cm²＋空白は12cm²＋？cm²より小さいので、？は1で
もない。

　？＝2cm²のとき、空白は6cm²。7cm²＋空白は12cm²＋？cm²より小さいので、？は2で
もない。

　？＝3cm²のとき、空白は8cm²。7cm²＋空白と12cm²＋？cm²は等しくなるので成り立つ。

　？＝4cm²のとき、空白は10cm²。

　？＝5cm²のとき、空白は12cm²。

　・・・・・・

　これ以後は、7cm²＋空白が12cm²＋？cm²より大きいので成り立たない。

　よって、黄色い部分は、3cm²


（コメント）　よおすけさん、正解です。いろいろな考え方が可能で、「面積迷路」問題は、素敵
　　　　　　ですね！


　カルピスさんからのコメントです。（平成２８年１２月２5日付け）

　稲葉さんの「算数パズルの部屋」の「お試し版」が４問あって全て解けるのですが、３番目
だけ、どうしても分数を使わないと私は解けないで泣いています。どうやったら「整数」だけで
解けますか？


　らすかるさんからのコメントです。（平成２８年１２月２5日付け）

　7cm×12cm=84cm²=26cm²+58cm²　により、58cm²の四角形を左端までずらすと、26cm²
の四角形とちょうど同じ幅で合う。よって、7cm。


　カルピスさんからのコメントです。（平成２８年１２月２６日付け）

　ひぇ〜、やっぱり、らすかるさんは大天才！！！これは思いつかなかったです。有難うござ
いました。


（コメント）　「お試し版」の解答が載っていないようなので私も解いてみました。

　（１）　１６cm²　　（２）　２２cm²　　（３）　７ｃｍ　　（４）　５１cm²

　「面積迷路」は頭の体操になりますね！今度、稲葉さんの本を買おうと思いました。


　カルピスさんからのコメントです。（平成２８年１２月２６日付け）

　「面積迷路」は、図を「わざと不正確」にしているのかなぁ〜。例えば、「８ｃｍ」よりも「４ｃｍ」
の方が、はるかに長かったり・・・・・。見た目で、直感が働かないよーにしているのかな？


　ｋｓさんからのコメントです。（平成２８年１２月２８日付け）

　こんなのがありました。小、大、中の順で、三つの正方形が接して並んでいます。小の正方
形から８�p足すと、大の高さになります。中の正方形から３ｃｍ足すと大の正方形になります。
下の並んだ長さが２５ｃｍです。大、中、小のそれぞれの面積を求めなさい。
（・・・小４レベルだそうです。）


　カルピスさんからのコメントです。（平成２８年１２月２８日付け）

　小・大・中　の順に、１６cm²・１４４cm²・８１cm² です。


　ｋｓさんからのコメントです。（平成２８年１２月２９日付け）

　カルピスさん、正解です。数学には、論理と直感が必要とのことですが、算数は直観的で、
数学は論理的ということでしょうか。年の瀬を迎え、以前の内容で十分に伝えきれない部分
がありました。「数学のすばらしさ」についてです。公理主義の限界とか。ガリレオの「自然は
数学の言葉で書かれている」がすべてなのか。５次以上の方程式が、すべては解けないこ
とが心に引っかかっています。超越数の表現の問題かもしれませんが。言葉に限界がある
ように、数学にも限界があるのではないかという趣旨です。あくまでも個人的な意見です。悪
しからず。


（コメント）　私は、方程式を立式して、小・大・中の正方形の一辺の長さが４ｃｍ・１２ｃｍ・９
　　　　　　ｃｍであることを求めましたが、小４レベルで解くとすれば次のように解くのでしょ
　　　　　　うか？

　　　　　　　　２５＋８＋３＝３６（ｃｍ）は、大の正方形の一辺の長さ３個分なので、小・大・中
　　　　　　の正方形の一辺の長さは、４ｃｍ・１２ｃｍ・９ｃｍとなる。よって、面積は、小・大・中
　　　　　　の順に、１６cm²・１４４cm²・８１cm² となる。