
当HPがいつもお世話になっているHN「SH」さんからHN「壊れた扉」さんの問題をご紹介
いただきました。(平成28年7月22日付け)
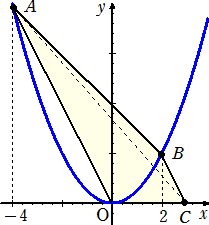
左図のように放物線 y=x2 上の2点A、Bに対して、x
軸上に△OAB=△OACとなるように点Cをとる。
このとき、点Bを通り、四角形OABCの面積を2等分す
る直線の方程式を求めよ。
(答) 壊れた扉さんによれば中学生用の問題とのことで、「数学好きな人は挑戦してみてく
ださい」ということなので挑戦してみました。(平成28年7月22日付け)
まず、A(−4,16)、B(2,4)で、直線AOの式は、 y=−4x
△OAB=△OACより、AOとBCは平行なので、直線BCの式は、 y=−4x+12
よって、 C(3,0) である。そこで、D(−1,4)をとると、点Dは直線AO上の点で、
四角形OABC=3×4+3×12÷2=30
となり、求める直線は、線分ADを5:1に分ける点(−3/2,6)を通る。
よって、 y=−(4/7)x+36/7
(コメント) 答えは合っているかな?
DD++さんからのコメントです。(平成28年7月22日付け)
四角形OBCDが平行四辺形になるように点Dを取ると、D(1,-4)
四角形OABC=三角形ABDなので、ADの中点M(-3/2,6)を通るように直接を引けばよく、
求める方程式は、 y=(-4/7)x+36/7
#実用的な解法って、これ1つしかないような...。2通りというのはこれに並ぶ簡素な計算
の別解があるのか、はたまた愚直に計算するのもやってほしい意図なのか……。
らすかるさんからのコメントです。(平成28年7月22日付け)
ほぼ同じですが、もう1通り。
四角形ABCDが平行四辺形になるように点Dを取ると、D(-3,12)
△ABD=△OBCなので、ODの中点M(-3/2,6)を通るように直接を引けばよく、求める方程式
は、y=(-4/7)x+36/7
DD++さんからのコメントです。(平成28年7月22日付け)
なるほど、そっちもありましたか。中点以外の内分点とか傾きを使って方程式とかは高校
入試としてはちょっと辛そう……。
(コメント) なるほど!DD++さん、らすかるさんの解答は何れも等積変形で四角形の面積を
三角形の面積に帰着させる方法ですね。感動しました。私の解法は、多分設問の
流れに従った解答と思われます。
S(H)さんからのコメントです。(平成28年7月22日付け)
A(−4,16)、B(2,4)で、直線AOの式は、 y=−4x
△OAB=△OACより、AOとBCは平行なので、直線BCの式は、 y=−4x+12
よって、 C(3,0) である。
このとき、四角形OABCの面積は、
(1/2)|(−4)・4−16・2|+(1/2)|2・0−4・3|=30
点B(2,4)を通り、四角形OABCの面積を2等分する直線の方程式は、傾きをmとして、
y=m(x−2)+4
直線 y=−4x との交点の座標は、D((2m−4)/(m+4),−4(2m−4)/(m+4))
△ABDの面積は、
(1/2)|(−6)・(−12m/(m+4))−12・(−12/(m+4))|=36|(m+2)/(m+4)|
よって、 36|(m+2)/(m+4)|=30/2 を解き、m=−4/7(適)、−44/17(不適)
以上から、求める直線は、 y=−(4/7)(x−2)+4=−(4/7)x+36/7