
当HPがいつもお世話になっているHN「GAI」さんからの出題です。
(平成27年6月8日付け)
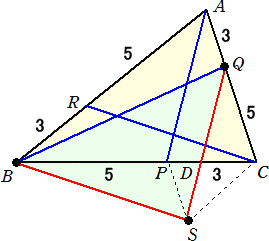
△ABCの各辺BC、CA、ABをそれぞれ5:3に内分する点をP、Q、Rとし、AP、BQ、CRの長
さの三辺を持つ三角形を作ると面積が196になった。
このとき、元の△ABCの面積は?
(答) S(H)さんから、答え「256」をいただきました。(平成27年6月8日付け)
S(H)さんからの続報です。(平成27年6月14日付け)
(1/2)Det{{ax, ay, 1}, {0, 0, 1}, {49/8 + (5 ax)/8, (5 ay)/8, 1}} = 196 を解き、ay=64
△ABC=(1/2)Det[{{ax, ay, 1}, {-5, 0, 1}, {3, 0, 1}}] に、ax=2、ay=64 を代入して、256 を得る。
GAI 様は如何されたのでしょうか?
GAI さんからのコメントです。(平成27年6月15日付け)
AB=b=(x1,y1)、AC=c=(x2,y2) で表しておくと、
AP=p=(1-t)b+tc (0<t<1) 、QB=q=b-(1-t)c
このとき、△ABCの面積L=Det[b,c]/2=|x1y2-x2y1|/2
一方、3つの長さで構成した三角形でAPの辺は固定して、BQの辺をQ→Aへ、CRの辺を
C→Pへ平行移動させできたものを△AB'P (B'はBが移動してできた頂点)とすると、この面積
K=Det[p,q]/2=(t2-t+1)|x1y2-x2y1|/2=(t2-t+1)L
t のいろいろな値に対して(内分する比として解釈)K、Lの関係を調べたら、
1:1 → K=3/4*L 、2:1 → K=7/9*L 、3:1 → K=13/16*L 、3:2 → K=19/25*L
4:1 → K=21/25*L 、4:3 → K=37/49*L 、5:1 → K=31/36*L 、
5:2 → K=39/49*L 、5:3 → K=49/64*L 、5:4 → K=61/81*L 、・・・・・・・・・・・・・・
これらの中で、数値的に面白かった「5:3」を選んで出題しました。
(コメント) 面白そうだったので計算してみた。
AB=8b、AC=8c とおくと、AQ=3c、AR=5b
このとき、 AS=8b+8c−5b=3b+8c なので、
BS=3b+8c−8b=−5b+8c
BQ=3c−8b
そこで、 |b|=m、|c|=n、∠BAC=θとおくと、 b・c=mncosθ
よって、|BS|2=25m2−80mncosθ+64n2
|BQ|2=64m2−48mncosθ+9n2
BS・BQ=(−5b+8c)・(3c−8b)=40m2−79mncosθ+24n2
より、
|BS|2|BQ|2−(BS・BQ)2=2401m2n2(1−cos2θ)=2401m2n2sin2θ
よって、 △BSQ=(49/2)mnsinθ となる。
問題の条件より、 (49/2)mnsinθ=196 なので、 mnsinθ=8 となる。
したがって、元の△ABCの面積Tは、
|AB|2=64m2、|AC|2=64n2、AB・AC=64mncosθ より、
4T2=4096m2n2−4096m2n2cos2θ=4096m2n2sin2θ なので、
2T=64mnsinθ より、 T=32mnsinθ=256 である。
(コメント) S(H)さんの結果と一致しているので、安心しました!ただ、計算が煩雑なのが
玉に瑕。図形的に解決することはできないものかと思案してみました
上図において、 APとQSは平行なので、PD:DC=AQ:QC=3:5
よって、 QD:DS=5:3
ACとPSは平行なので、BD:DC=5+9/8:15/8=49:15
△BSQ=196 なので、 △BDQ=196×(5/8)=245/2
△BCQ=(245/2)×(64/49)=160 より、 △ABC=160×8/5=256
(コメント) こちらの初等幾何的解法の方が簡単でした!
(追記) 三角形の縮小群と題して、GAI さんからの続報です。(平成27年6月16日付け)
面積1の△ABCの辺AB、AC上に、s:1-s、t:1-t の比にそれぞれ内分する点をD、Eとす
る。(0<s、t<1) 線分CD、BEの交点をPとするとき、△ABCは5つの三角形△ADE、△BDP、
△CEP、△BCP、△DEPに分かれる。
このとき、それぞれの面積を s、t で表せ。また、この5つの三角形がみんな同じ面積にな
ることはあるか?
S(H)さんから答をいただきました。(平成27年6月16日付け)
それぞれ st 、(-t+2st-s2t)/(-1+st)、(-s+2st-st2)/(-1+st)、-(-1+s)(-1+t)/(-1+st)、
(-st+s2t+st2-s2t2)/(-1+st)
公平に分けることが叶うか?
(コメント) 面白そうだったので計算してみた。
AD:DB=s:1−s 、AE:EC=t:1−t 、△ADE=x とおくと、
△BDP=(1−s)2x/{s(1−st)}、△CEP=(1−t)2x/{t(1−st)}、
△BCP=(1−s)(1−t)x/{st(1−st)}、△DEP=(1−s)(1−t)x/(1−st)
△ADE+△BDP+△CEP+△BCP+△DEP=1 なので、 x/(st)=1 より、 x=st
よって、 △ADE=st 、 △BDP=(1−s)2t/(1−st)、△CEP=(1−t)2s/(1−st)、
△BCP=(1−s)(1−t)/(1−st)、△DEP=(1−s)(1−t)st/(1−st)
(S(H)さんの結果と一致して安心しました!)
試しに、 st=(1−s)(1−t)st/(1−st) と置いてみると、 (2s−1)(2t−1)=1
この等式を満たす s、t は、0<s、t<1の範囲には存在しない。
よって、5つの三角形がみんな同じ面積になることはない。
KSさんからのコメントです。(平成27年6月17日付け)
三角形の内分点で作る内部の三角形の面積を計算する公式を作ってみました。
△ABCの面積をTとする。AB、BC、CAの内分点の比を、1:n1、1:n2、1:n3 とし、頂点
AとBCの内分点、頂点BとCAの内分点、頂点CとABの内分点を結び、中にある囲まれた三
角形の面積をSとすると、一般に、次の式で与えられる。
S=(1/3){(1−2n1+n1n2)/(1+n1+n1n2)
+(1−2n2+n3n2)/(1+n2+n3n2)+(1−2n3+n1n3)/(1+n3+n1n3)}T
したがって、よくある1:2の内分で作られる三角形の比は、元の三角形の面積の7分の1
となることが分かります。
平行四辺形ABCDの面積をTとする。辺AB、BC、CD、DAの内分点の比を、それぞれ
1:m1、1:m2、1:m3、1:m4 とし、頂点AとBCの内分点、頂点BとCDの内分点、頂点C
とDAの内分点、頂点Dと辺ABの内分点を結び、中に囲まれる四角形の面積をSとすると、
一般に、次の式が得られる。
S=(1/4){(m1−m2+m1m2)/(2+m1+m2+m1m2)
+(m2−m3+m2m3)/(2+m2+m3+m2m3)
+(m3−m4+m3m4)/(2+m3+m4+m3m4)
+(m4−m1+m4m1)/(2+m4+m1+m4m1))}T
特に、正方形の中点を結ぶと、元の5分の1となります。
(生徒からの質問で難儀したので、公式化しました。)