当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（平成２７年５月１６日付け）
ａ＞０、ｂ＞０、ｃ＞０ とする。２次方程式 ａｘ2＋ｂｘ＝ｃ の正の解を、図形の面積を利用し
て求めよ。
（答） よおすけさんから解答をいただきました。（平成２７年５月１８日付け）
図は省略しますが、ｘ の値は、 x=(-b＋√(b2＋4ac))/(2a) ※ ただし、a≠0
（コメント） 図を補足しました。
１辺の長さが ｂ/（２ａ）の正方形を考え、１辺の長さをｘだけ増やして、もっと広い面積の正
方形を作る。そのときの面積の増加量が、ｃ/ａ である。
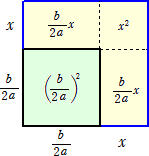左図において、 ｘ2＋（ｂ/ａ）ｘ＝ｃ/ａよって、 ｘ2＋（ｂ/ａ）ｘ＋（ｂ/２ａ）2＝ｃ/ａ＋（ｂ/２ａ）2 から、
（ｘ＋ｂ/２ａ）2＝ｃ/ａ＋（ｂ/２ａ）2 （← 正方形の面積）
これより、よおすけさんの結果を得る。
（参考文献： 遠山 啓 著 「数学入門 （上）」 （岩波新書） ｐ．１８８〜ｐ．１９３）
らすかるさんから補足をいただきました。（平成２７年５月２３日付け）
ａｘ2＋ｂｘ＝ｃ の大きい方の解は、x=(-b+√(b2+4ac))/(2a)＞(-b+b)/(2a)=0 なので、正に
なります。