
次の問題は、数学が得意な人も悩ませる良問である。幅広い考え方が要求される。
下図において、ひし形OABCの面積を直線DEが2等分するとき、Eの座標を求めよ。
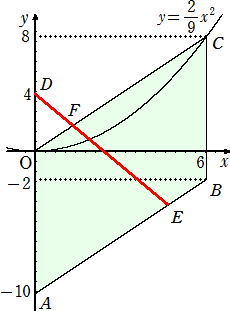
(答) ひし形OABCの面積は、10×6=60なので、その半分は、30
△OFD∽△AEDで、相似比は、4:14=2:7
よって、 △OFD:△AED=22:72=4:49 なので、△OFD=Sとおくと、
S:S+30=4:49 より、 49S=4(S+30) なので、 S=8/3
以上より、 △AED=8/3+30=98/3
点E(x,y)とすると、 14x/2=98/3 なので、 x=14/3
直線ABの方程式は、 y=(4/3)x−10 より、 y=(4/3)(14/3)−10=−34/9
よって、E(14/3,−34/9)である。 (終)
この解答を掲載した後、いろいろな方から別解を頂いた。別解を拝見させていただいて、
上記の解が大袈裟すぎるテクニックに走ってしまったと反省すること然りである。別解をお
寄せいただいた方々に感謝します。
DD++さんからのコメントです。(平成27年2月18日付け)
線分OBの中点をMとして、線分ABと直線DMとの交点を求めればいいだけでは...。平行
四辺形(もちろん菱形でもよい)において、「直線が面積を二等分 <=> 直線が対角線の中点
を通る」なので。
(コメント) 確かに、その通りでした!
S(H)さんからのコメントです。(平成27年2月18日付け)
Integrate[(8/6)*x - ((8/6)*x - 10), {x, 0, -(12/(-4 + 3 m))}] +
Integrate[(m*x + 4) - ((8/6)*x - 10), {x, -(12/(-4 + 3 m)), -( 42/(-4 + 3 m))}]
=-(270/(-4 + 3 m))
-(270/(-4 + 3 m)) = (1/2)*10*6 より、 m= -(5/3)
よって、 {-(42/(-4 + 3 m)), m*(-(42/(-4 + 3 m))) + 4} /. m -> -5/3 = {14/3, -(34/9)}
KSさんからのコメントです。(平成27年2月18日付け)
平行四辺形の直線による分割は、中点を通るように引けばよい。そのような場合を考えて
みました。まず円がそうですね。それから、偶数の多角形が中心を、通る直線はその面積を
二等分する。それから、奇数の正多角形を二つ重ね、一つを百八十度回転させた、星形図
形も中心を通ればよい。他にもあるでしょうか?
らすかるさんからのコメントです。(平成27年2月18日付け)
点対称かつ1本の直線で三つ以上に分かれない図形なら何でも良いので、楕円、トラック
型、歯が偶数の歯車型や、条件を満たす図形を複数個重ねた図形など、いくらでもあります
ね。
より一般には、f(x)が0≦x≦2πで定義されたf(x)=f(x+π)である正値関数で、r=f(θ) (連
続でない箇所は線分で結ぶことにする)で囲まれる図形が条件を満たします。
(ただし、これは十分条件でしかありません。)
S(H)さんからのコメントです。(平成27年2月18日付け)
中心を通ればよい。他にもあるでしょうか? 直線による分割は...。
In[1]:= (1/4)*{0, 0} + (1/4)*{0, -10} + (1/4)*{6, -2} + (1/4)*{6, 8}
y == m*x + 4 /. {x -> %[[1]], y -> %[[2]]}
Solve[%, m] {-(42/(-4 + 3 m)), -((2 (8 + 15 m))/(-4 + 3 m))} /. %
Out[1]= {3, -1}
Out[2]= -1 == 4 + 3 m
Out[3]= {{m -> -(5/3)}}
Out[4]= {{14/3, -(34/9)}} (← 「重心」思考)
カルピスさんからのコメントです。(平成27年2月18日付け)
私もDD++さんの方法でやってみました。大賛成です。
通りすがりさんからのコメントです。(平成27年2月19日付け)
対角線OBと対角線ACの交点をMとすると、M(3,-1) 条件を満たすのは、直線DEが点M
を通るときなので、DE: 5x+3y=12 また、AB: 4x-3y=30
よって、辺ABと直線DEの交点Eは、(14/3,-34/9)である。
らすかるさんからのコメントです。(平成27年2月19日付け)
直線の方程式を使わず図形的に解く別解。
直線DEと直線BCの交点Pはひし形OABCの対角線の交点(3,-1)に関して、Dと対称な点
なのでP(6,-6)
△EDA∽△EPBで、相似比は、DA:PB=14:4=7:2 なので、Eは、ABを7:2に内分する点、
すなわち、 (14/3,-34/9)
(コメント) らすかるさんの別解に刺激されて、次のような解も有りでしょう。
(解) 直線OCの方程式は、y=(4/3)x である。Fは点D(0,4)とひし形の対角線の交点
G(3,−1)を結ぶ線分を4:5に内分する点なので、F(4/3,16/9)
よって、線分EFの中点がG(3,−1)となるので、E(x,y)とすると、
(4/3+x)/2=3 、(16/9+y)/2=−1
このとき、 x=6−4/3=14/3 、y=−2−16/9=−34/9 なので、
E(14/3,−34/9)である。 (終)