次の問題は、非常に素朴な感じに思えるが、意外と手強い。小学生・中学生では難しいと感
じるであろう。小学生・中学生が習う範囲の解き方で出来た方は、是非塾長宛メールを下さい。
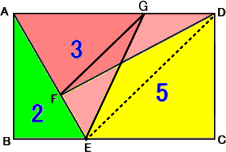
縦・横の長さが不明な長方形ABCDがある。BC上の点EとAを結ぶ線分AE上に点Fをとり、
線分DFを引くと、△ABE:△ADF:四角形ECDF=2:3:5 であった。このとき、AF:FE は
いくらになるか?

(答) 3:2
(追記) 結論から言えば、この問題は小学生には厳しいが、中学生には適度な思考力が
あれば十分解決できるレベルの問題というように、冒頭を訂正したいと思う。
当初、予定した解答は以下の通りである。
 BE=2 とすると、△ABE=2 から、AB=2
BE=2 とすると、△ABE=2 から、AB=2(普段、辺の長さから面積を求めているが、面積から
辺の長さを指定することは、多分新鮮な発想だろう!)
このとき、EC=X とおくと、台形AECDの面積から、
(X+X+2)・2・(1/2)=8 が成り立ち、X=3 である。
よって、△DEC=3・2・(1/2)=3 より、
△DEF=5−3=2 となる。
従って、AF:FE=△DAF:△DEF=3:2 である。
これに対して、柳本さんという方から、次のような解を頂戴した。
小学生・中学生が習う範囲の解き方で出来たかどうかはわかり ませんが、次の様に考
えることができます。ちょっと長くなり ますが、ご容赦を。
1) Eより辺ADに垂線をおろし、その足をGとする。△ABEの面積が2だから、
長方形ABEGの面積は4となる。
2) DEを結ぶ。長方形DCEGの面積は6だから、△DECの面積は3。
よって△EDFの面積は2
3) △ADF:△EDF=3:2になる。この2つの三角形の底辺をAFとEFと考えると、
高さは等しいので、面積の違い(比?)は底辺の違い(比?)だけとなる。
よって、AF:FE=3:2
方程式を使わずに、△DEC=3 が示せたのは、十分小学校的だと思います。高さが等し
い三角形の面積比が底辺の比という事実は、十分小学生でも理解できますよね?
解答をお寄せいただいた柳本さんに感謝いたします。
(追々記) 「当初予定した解答」について、「BE=2」のときは、確かに「AF:FE=3:2」で
あるが、一般のBEの長さに対しても、「AF:FE=3:2」であろうか?というご指摘
を頂いた。このご指摘は、至極もっともなご指摘であるので、上記解答の不備を、
下記のように修正したいと思う。
△ABE:△ADF:四角形ECDF=2:3:5 より、AB=a を用いて、
△ABE=2aS 、△ADF=3aS 、四角形ECDF=5aS (S は比例定数)
と書ける。このとき、 a×BC=10aS より、BC=10S 。
また、△ABE=2aS=(1/2)・a・BE より、BE=4S 。このとき、EC=6S となる。
よって、△DEF=(1/2)・a・6S=3aS なので、△DEF=5aS−3aS=2aS
従って、AF:FE=△DAF:△DEF=3aS:2aS=3:2 である。
(追々々記) 平成17年2月20日に、i-k さんという方から、非常に小学生的な解答をお寄
せいただいた。ちょっと今まで難しく考えすぎていたみたいです...。
長方形ABCDの面積が、10 なので、△AEDの面積は、5。
よって、△FEDの面積は、2 となる。このとき、高さが等しい三角形の面積比は底辺の比
に等しいので、AF : FE=3 : 2 となる。
解答をお寄せいただいた、i-k さんに感謝いたします。
(追記) 平成22年2月17日付け
2月16日付けで、ある方からメールを頂いた。(一部文言等を修正させていただきました!)
面積比の問題、受験を目指すような小学5・6年生、あるいは中学1年生ならば十分に解
けるのではないでしょうか。
ADに垂直なFを通る直線をBCまで引き、ADとの交点をG、BCとの交点を I とする。長方
形全体の面積は、2k+3k+5k=10k (k は比例定数)である。
△ADFの面積は、AD×GF/2=3k で、また、△ADI の面積は、AD×GI/2=5k であ
る。このとき、 GI : GF = 5 : 3 となる。
したがって、 AF : FE = GF : FI = 3 : 2 となる。
(コメント) 解法の大筋は、上記の i-k さんのものと同じですね!
(追記) 平成23年11月8日付けで、T.A.さんからメールを頂いた。
うちの娘(小5)だとこんな解き方です。合ってますか?
△ABE は、□ABCDの面積の1/5 従って、BEはBCの長さの2/5
BE:EC=2:3 なので、△ABEの面積:△ECDの面積=2:3
□ECDFから△ECDを引いて、△FEDの面積:△ECDの面積=2:3
△AFDと△ECDの面積は等しいので、△AFDの面積:△FEDの面積=3:2
この2つは高さの等しい三角形の底辺であるため、AF:FE=3:2
(コメント) 正解です!面積比から辿っていって結論を得ていますので正に模範解答です。
さらに、T.A.さんから、もっと簡単だという解を頂いた。
△AED は □ABCDの面積の1/2 →□ABCDの面積を10とすると5
△FEDの面積=△AEDの面積-△AFDの面積=5-3=2
△AFDの面積:△FEDの面積=3:2
この2つは高さの等しい三角形の底辺であるため、AF:FE=3:2
(コメント) この解は、上記の「i-k さんの解答」と同じです。もっとも易しいと思われる解に
辿り着かれましたね!
(追記) 平成23年12月16日付けで、J.Y.さんから別解をメールで頂いた。