
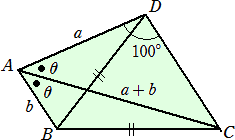
 丂丂巐妏宍俙俛俠俢偵偍偄偰丄佢俙俢俠亖侾侽侽亱偱丄
丂丂巐妏宍俙俛俠俢偵偍偄偰丄佢俙俢俠亖侾侽侽亱偱丄丂丂丂俛俢亖俛俠丄俙俠亖俙俢亄俙俛丄佢俛俙俠亖佢俢俙俠
丂偺偲偒丄佢俛俙俢偺戝偒偝傪媮傔傛丅
乮嶲峫丗拀攇戝妛晬懏嬵応崅峑悢妛壢妛尋媶夛曇丂乽俠倎倖倕丂俛倧倢倢倵倕們倠丂俶倧丏嘮乿乯
乮摎乯丂梋尫掕棟傛傝丄丂俛俠2亖乮倎亄倐乯2亄倐2亅俀倐乮倎亄倐乯們倧倱兤
丂丂丂丂丂丂丂丂丂丂丂俛俢2亖倎2亄倐2亅俀倎倐們倧倱俀兤
丂忦審傛傝丄俛俢亖俛俠丂側偺偱丄倎2亄倐2亅俀倎倐們倧倱俀兤亖乮倎亄倐乯2亄倐2亅俀倐乮倎亄倐乯們倧倱兤
丂幃傪惍棟偟偰丄丂係倎們倧倱2兤-俀乮倎亄倐乯們倧倱兤亄倐亖侽
丂丂乮俀們倧倱兤亅侾乯乮俀倎們倧倱兤亅倐乯亖侽丂傛傝丄丂們倧倱兤亖侾/俀丂丄倐/乮俀倎乯
丂們倧倱兤亖侾/俀丂偺偲偒丄兤亖俇侽亱偐傜丄佢俛俙俢亖俀兤亖侾俀侽亱丂偲側傞丅
丂們倧倱兤亖倐/乮俀倎乯丂偺偲偒丄
丂丂俠俢2亖乮倎亄倐乯2亄倎2亅俀倎乮倎亄倐乯們倧倱兤亖乮倎亄倐乯2亄倎2亅倐乮倎亄倐乯亖俀倎2亄倎倐
丂偙偙偱丄丂們倧倱侾侽侽亱亖乮倎2亄俠俢2亅乮倎亄倐乯2乯/乮俀倎丒俠俢乯亖乮俀倎2亅倎倐亅倐2乯/乮俀倎丒俠俢乯
丂偙偺幃傛傝丄倎丄倐偺斾椺幃偑媮傑傝丄偦偺寢壥偲偟偰丄們倧倱兤亖倐/乮俀倎乯偺抣偑掕傑傝丄兤
偑妋掕偡傞傢偗偩偑丄兤偼嬶懱揑偵婰弎偱偒傞偺偩傠偆偐丠
丂忋婰偺壽戣傪傜偡偐傞偝傫偑夝寛偝傟傑偟偨丅傜偡偐傞偝傫偵姶幱偟傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俇擭侾寧係擔晅偗乯
丂們倧倱兤亖倐/乮俀倎乯亖倲丂偲偍偔偲丄俠俢2/倎2亖俀亄俀倲
丂們倧倱侾侽侽亱亖乮俀亅倐/倎亅倐2/倎2乯/乮俀俠俢/倎乯亖乮俀亅俀倲亅係倲2乯/乮俀俠俢/倎乯
丂丂丂丂丂丂丂丂亖乮侾亅倲亅俀倲2乯/乮俠俢/倎乯亖乮侾亅俀倲乯乮侾亄倲乯/乮俠俢/倎乯
丂偙偙偱丄們倧倱侾侽侽亱亙侽丂側偺偱丄侾亅俀倲亙侽丂傛傝丄們倧倱兤亜侾/俀丂偲側傝丄兤亙俇侽亱乧(*)
丂傑偨丄丂們倧倱2侾侽侽亱亖乮侾亅俀倲乯2乮侾亄倲乯2/乮俠俢2/倎2乯亖乮侾亅俀倲乯2乮侾亄倲乯2/乮俀亄俀倲乯
丂丂丂丂丂丂丂丂丂丂丂丂丂亖乮侾亅俀倲乯2乮侾亄倲乯/俀
傛傝丄丂俀們倧倱2侾侽侽亱亖乮侾亅俀倲乯2乮侾亄倲乯亖係倲3亅俁倲亄侾丂側偺偱丄們倧倱俀侽侽亱亖係倲3亅俁倲
丂偲偙傠偱丄係倲3亅俁倲亖係們倧倱3兤亅俁們倧倱兤亖們倧倱俁兤丂側偺偱丄們倧倱俁兤亖們倧倱俀侽侽亱
丂乮*乯傛傝丄侽亱亙兤亙俇侽亱側偺偱丄丂侽亱亙俁兤亙侾俉侽亱
丂偙偺斖埻偱丄丂們倧倱俁兤亖們倧倱俀侽侽亱傪夝偔偲丄丂俁兤亖侾俇侽亱傛傝丄丂兤亖侾俇侽亱/俁
丂偟偨偑偭偰丄丂佢俛俙俢亖俀兤亖俁俀侽亱/俁丂偲側傞丅
乮僐儊儞僩乯丂搑拞寁嶼偱丄俀攞妏偺岞幃偺傒側傜偢丄俁攞妏偺岞幃傕搊応偟偰丄埑搢偝傟傑偟
丂丂丂丂丂丂偨丅傛偔峫偊傜傟偨栤戣偲偄偆偙偲偱偟傚偆偐丏丏丏丅