当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（令和７年１０月２日付け）
問題 中心Ｏの定円に内接し、点Ｏを内部に含む四辺形ＡＢＣＤを
(１) ∠ＡＯＢ=６０° (２)∠ＡＯＤ＋∠ＢＯＣ=１８０°
となるようにとり、直線ＡＤと直線ＢＣとの交点をＰとする。いま、Ａ、Ｂを固定して、条件(２)を
満たしながら、Ｃ、Ｄを動かすとき、線分ＡＰが最大になるのは、∠ＡＯＤが何度のときか。
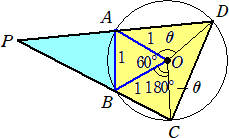
（出典） 大阪大学前期理系・文系(１９６２)
（答） 円Ｏの半径は、１としても一般性を失わない。
∠ＡＯＤ＝θ とおくと、（２）から、∠ＢＯＣ＝１８０°−θ となる。
円周角の大きさは中心角の大きさの半分なので、 ∠ＢＣＤ＝（６０°＋θ）/２
同様に、 ∠ＡＤＣ＝（６０°＋１８０°−θ）/２＝（２４０°−θ）/２
このとき、 ∠ＡＰＢ＝１８０°−（６０°＋θ）/２−（２４０°−θ）/２＝３０° となる。
また、ＡＤ＝２ｓｉｎ（θ/２） 、ＢＣ＝２ｓｉｎ（（１８０°−θ）/２）＝２ｃｏｓ（θ/２） である。
△ＡＢＰにおいて、余弦定理より、
１＝ＡＰ2＋ＢＰ2−２ＡＰ・ＢＰｃｏｓ３０°＝ＡＰ2＋ＢＰ2−
ＡＰ・ＢＰ ・・・ （*）∠ＣＯＤ＝１２０° より、 ＣＤ＝
であるので、△ＰＡＢ∽△ＰＣＤ より、ＡＰ ： １＝ＢＰ＋２ｃｏｓ（θ/２） ：
なので、 ＢＰ＝ＡＰ−２ｃｏｓ（θ/２）これを、（*）に代入して整理すると、ＡＰ2−２
ｃｏｓ（θ/２）・ＡＰ＋４ｃｏｓ2（θ/２）−１＝０よって、 ＡＰ＝
ｃｏｓ（θ/２）±ｓｉｎ（θ/２） と書ける。０°＜θ＜１８０° から、 ０°＜θ/２＜９０°
最大値を持つのは、 ＡＰ＝
ｃｏｓ（θ/２）＋ｓｉｎ（θ/２）＝２ｓｉｎ（θ/２＋６０°） のときで、 θ/２＋６０°＝９０° から、 θ＝６０° （終）
以下、工事中！