当ＨＰがいつもお世話になっているＨＮ「よおすけ」さんからの出題です。
（令和７年８月５日付け）
問題 ∠Ａ＝９０°、ＡＢ＞ＡＣ である直角三角形ＡＢＣの∠Ａの２等分線が対辺ＢＣおよび
△ＡＢＣの外接円と交わる点をＤおよびＥとする。
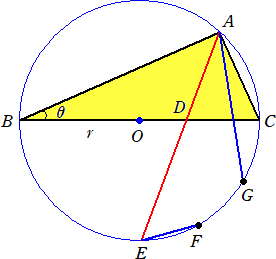
（１） ∠Ｂ＝θとして、線分ＡＥ、ＤＥの長さを、θおよび△ＡＢＣの外接円の半径 ｒ を用いて
表わせ。
劣弧ＥＣの３等分点のうち、Ｅに近い方をＦ、Ｃに近い方をＧとし、２ＡＤ＝ＤＥとするとき、
（２）、（３）に答えよ。
（２） θは何度か。
（３） ＡＢとＥＦは平行で、ＡＧとＢＣは直交することを証明せよ。
（出典） 東北大学（１９６１）
（答） （１） ＢＣ⊥ＯＥ なので、 ∠ＡＯＥ＝９０°＋２θ である。
△ＡＯＥ において、余弦定理より、
ＡＥ2＝ｒ2＋ｒ2−２ｒ2ｃｏｓ（９０°＋２θ）＝２ｒ2（１＋ｓｉｎ２θ）
よって、 ＡＥ＝
ｒ√（１＋ｓｉｎ２θ） となる。また、ＡＢ＝２ｒｃｏｓθ 、ＡＣ＝２ｒｓｉｎθ なので、 △ＡＢＣ＝２ｒ2ｓｉｎθｃｏｓθ＝ｒ2ｓｉｎ２θ
このとき、（１/２）ＡＤ・２ｒｃｏｓθ・ｓｉｎ４５°＋（１/２）ＡＤ・２ｒｓｉｎθ・ｓｉｎ４５°＝ｒ2ｓｉｎ２θ
すなわち、 ＡＤ・（ｒ/
）（ｓｉｎθ＋ｃｏｓθ）＝ｒ2ｓｉｎ２θ から、ＡＤ＝
ｒｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ）よって、 ＤＥ＝
ｒ（√（１＋ｓｉｎ２θ）−ｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ）） となる。（２） ２ＡＤ＝ＤＥ より、
２
ｒｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ）＝ｒ（√（１＋ｓｉｎ２θ）−ｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ））すなわち、 ２ｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ）＝√（１＋ｓｉｎ２θ）−ｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ）
より、 ３ｓｉｎ２θ/（ｓｉｎθ＋ｃｏｓθ）＝√（１＋ｓｉｎ２θ） 即ち、
３ｓｉｎ２θ＝（ｓｉｎθ＋ｃｏｓθ）√（１＋ｓｉｎ２θ）
両辺を平方して、 ９ｓｉｎ2２θ＝（１＋ｓｉｎ２θ）2 から、 （４ｓｉｎ２θ＋１）（２ｓｉｎ２θ−１）＝０
０＜θ＜π/２ なので、 ４ｓｉｎ２θ＋１≠０ より、 ｓｉｎ２θ＝１/２
よって、 ２θ＝π/６ から、 θ＝π/１２
（３） ∠ＡＥＣ＝１５° で、∠ＣＥＦ＝３０°から、∠ＡＥＦ＝４５°
よって、錯角が等しいので、 ＡＢとＥＦは平行 である。
また、ＡＧとＢＣの交点をＨとすると、
∠ＡＨＢ＝９０° となるので、ＡＧとＢＣは直交する。 （終）
（コメント） （１）（２）がクリア出来れば、（３）はおまけ的問題でした。
以下、工事中！