
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和6年5月16日付け)
下図のように、正方形の中に半円と四分円がある。角θの大きさを求めよ。
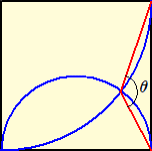
(出典)【角度当てクイズ Vol.806】 x の角度は何度?(エキサイトニュース)
(答) θ=135°
実際に、下図のように、2円の交点をPとし、線分AP、BP、DPを考える。
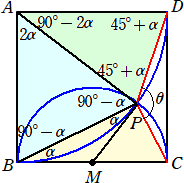
∠MBP=α とおくと、接弦定理と中心角の定理から、 ∠BAP=2α である。
また、△ABPは2等辺三角形なので、 ∠ABP=∠APB=90°−α
∠PAD=90°−2α で、△APDは2等辺三角形より、 ∠APD=∠ADP=45°+α
よって、 ∠BPD=(90°−α)+(45°+α)=135° となる。
したがって、 θ=360°−135°−90°=135° である。 (終)
(コメント) 円周角BADの中心角は270°なので、 ∠BAD=135° であることは、上
記の計算をしなくても直ぐ分かるんですね!
(追記) 令和6年5月17日付け
交点Pの持つ性質について、少し調べてみよう。

A(0,2)を中心とする半径2の四分円 x2+(y−2)2=4 と、M(1,0)を中心とする半径
1の半円 (x−1)2+y2=1 の交点Pの座標は、連立して、y=(1/2)x なので、
P(8/5,4/5) となる。直線CPの方程式は、傾きが −(4/5)/(2−(8/5))=−2 より、
y=−2(x−2)=−2x+4 となり、 辺ADとN(1,2)で交わる。よって、Nは辺ADの中点
となる。直線BPの方程式が y=(1/2)x なので、辺CDと点L(2,1)で交わる。よって、Lは
辺CDの中点となる。
さらに、直線APの方程式は、傾きが ((4/5)−2)/(8/5)=−3/4 より、
y=−(3/4)x+2 である。
ところで、 円 (x−1)2+y2=1 上の点P(8/5,4/5)における接線の方程式は、
(x−1)(8/5−1)+(4/5)y=1 すなわち、 3x+4y=8 から、 y=−(3/4)x+2
したがって、直線APは、円 (x−1)2+y2=1 上の点Pを接点とする接線となっている。
接弦定理から、 ∠BPA=∠BCP=90°−α で、直線BPと直線CPは垂直なので、
∠APN=α となる。よって、△QPNは、QP=QNの2等辺三角形になる。
このことから、 ∠DPN=45° であることが分かる。
したがって、 θ=180°−45°=135° である。
# ∠DPN=45° であることは、
∠DPN=180°−(90°−α)−(45°+α)=45° からも分かる。
(コメント) △QPNは、QP=QNの2等辺三角形になるんですね!何となく、問題作成に
使えそう...。
以下、工事中!