
正方形ABCDにおいて、辺CD上に点Eをとり、∠BEC=73°とする。また、辺AD上に
点Fをとり、∠AFB=62°とする。このとき、∠DEFの大きさを求めよ。
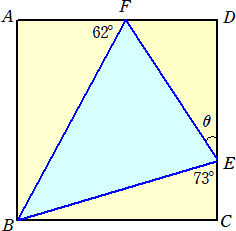
(答) 34°
実際に、下図において、△BCE≡△BAGとなる点Gをとる。
角の大きさ(30) 
正方形ABCDにおいて、辺CD上に点Eをとり、∠BEC=73°とする。また、辺AD上に
点Fをとり、∠AFB=62°とする。このとき、∠DEFの大きさを求めよ。

(答) 34°
実際に、下図において、△BCE≡△BAGとなる点Gをとる。
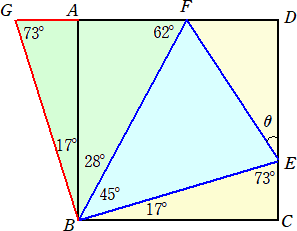 |
このとき、BF共通で、 BE=BG、∠EBF=∠GBF=45° から、2辺夾角相等で、 △BEF≡△BGF である。 よって、 ∠BEF=73°なので、 θ=180°−73°×2=34° となる。 |
(コメント) 45°の特殊性から、 ∠BFA=∠BFE 、∠BEF=∠BEC となる点が面白
いですね!
以下、工事中!