
正方形ABCDにおいて、辺CD上に点Eをとり、線分AEと対角線BDの交点をFとする。
いま、EC=EFであるとき、∠AFBの大きさを求めよ。
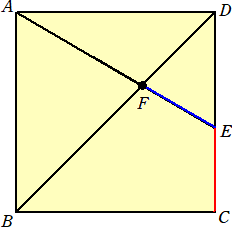
(答) 75°
実際に、次のような図を考える。
角の大きさ(29) 
正方形ABCDにおいて、辺CD上に点Eをとり、線分AEと対角線BDの交点をFとする。
いま、EC=EFであるとき、∠AFBの大きさを求めよ。

(答) 75°
実際に、次のような図を考える。
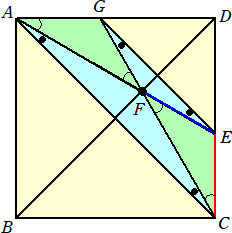 |
線分CFの延長と辺ADの交点をGとする。 このとき、EGとACは平行で、△CEF≡△AGF より、 △EFG、△AFCは2等辺三角形となる。 よって、∠FAC=∠FCA=θとおくと、 ∠FEG=∠FGE=θで、∠FAG=∠AFG=2θ このとき、 ∠CAG=3θ=45°より、θ=15° |
よって、 ∠AFB=90°−15°=75°となる。
(コメント) 当初、条件「EC=EF」をどう使うか思案しましたが、対角線BDに関して対称移
動させると、一気に視界が開けました!
よおすけさんからのコメントです。(令和4年1月14日付け)
別の視点で興味があったので...。
EG//DA//BCとなるように辺AB上に点Gを取り、2つの線分DGとAEの交点をHとすると、
△DHEは、DH=ED かつ ∠HDE=60°の二等辺三角形。
これから順次割り出せば、∠AFB=180°-∠DFH=∠DHF+∠HDF=75°
ただし、「△DHEは2等辺三角形」を証明していないので、完全な解答ではありません。
(コメント) よおすけさんの視点で、「△DHEは2等辺三角形」を証明しようと試みましたが、
出来ませんでした。
ただ、下図からも分かる通り、結果的には、△DHEは正三角形になるんですね!
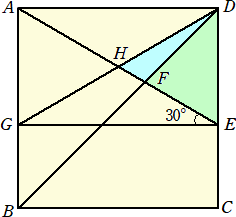
DD++ さんからのコメントです。(令和4年1月14日付け)
「長方形 ADEG の対角線の長さは等しく、H は各対角線の中点だから」じゃダメなんでしょ
うか?
よおすけさんからのコメントです。(令和4年1月14日付け)
Hが2つの線分DGとAEの中点ということに気づきませんでした。確かにそうです。
DD++ さんからのコメントです。(令和4年1月14日付け)
ところで、どっちかというと、「∠HDE=π/3」の方が根拠がない気がしますが、これ、どこか
ら来たんでしょう?
よおすけさんからのコメントです。(令和4年1月15日付け)
長方形ADEGの対角線の長さは等しく、Hは各対角線の中点だから、AH=HE=DH=HG
もし、辺EDが上の4つの線分と等しければ、△DHEの3辺はすべて等しくなるので、
∠HDE=π/3
DD++ さんからのコメントです。(令和4年1月15日付け)
その ED の長さが等しいというのは、どこから……?
よおすけさんからのコメントです。(令和4年1月17日付け)
EG//DA//BCとなるように辺AB上に点Gを取り、2つの線分DGとAEの交点をH、対角線BD
と線分EGとの交点をIとする。
Hが2つの線分DGとAEの中点なので、△DHEは、DH=EH
続き。途中までです。
DJ=JGとなるように線分EG上に点Jを取ると、△DGJは∠DGJ=∠GDJの二等辺三角形。
これより、∠DJE=∠DGJ+∠GDJ かつ ∠DGJ=∠GDJより、∠DJE=2∠DGJ
ここで、∠HDJの二等分線と線分GEの交点をK...と言いたいですが、この二等分線は対角
線BDとかぶってしまったため、ここから先が進めなくなりました。
※勝手に「対角線BDは∠HDJの二等分線」を使うことができないため
(コメント) 「DH=ED」が言えれば、△DHEが正三角形となり、無問題なのですが、
「DH=ED」が簡単に説明できないところが問題ですね!
よおすけさんからのコメントです。(令和6年5月22日付け)
今日、エキサイトニュースの角度当てクイズを見ていたら、
【角度当てクイズ Vol.225】 x の角度は何度?(2023年5月28日 13:00投稿)
が、冒頭の問題と同じ問題でした。
角度当てクイズの公式解答には、下図がありました。
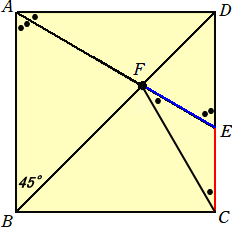
(図の補足説明) ∠DCF=● とすると、∠DABは、●が3つ分であることがわかります。
すなわち、●×3=90°より、●=30°となる。
よって、 ∠AFB=180°−45°−60°=75°
(コメント) よおすけさんの補足を更に補足させていただくと、
△ADFと△CDFにおいて、 AD=CD 、DFは共通 、∠ADF=∠CDF=45° なので、
2辺夾角相等で、△ADF≡△CDF となる。よって、∠FAD=∠FCD=● であることが分
かります。この確認は、必要ですね!
以下、工事中!