
下図のような△ABCにおいて、Oは△ABCの外心、DはOから辺ABに下ろした垂線の足、
AEは∠Aの2等分線、FはAから辺BCに下ろした垂線の足とする。
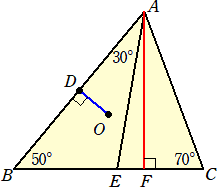
このとき、∠AOB、∠AOD、∠OAE、∠EAFの大きさをそれぞれ求めよ。
(答) ∠AOB=140°、∠AOD=70°、∠OAE=10°、∠EAF=10°
PBさんからのコメントです。(令和2年6月9日付け)
上記で、∠AOEを求めるのも面白い問題になると思います。
(解) BCに関して、点Oの対称な点Pをとると、△OBPは正三角形で、Oは△ABPの外心で
もある。よって、∠ABP=80°より、∠AOP=160°なので、∠OAP=10°
ところで、∠OAE=10°なので、∠OAP=∠OAE となり、3点A、E、Pは同一直線上にある。
したがって、∠PDE=10°なので、∠AOE=160°ー10°=150° (終)
(コメント) もともとの問題とは比較にならない位の良問で、難問ですね!勉強になりました〜!
PBさんに感謝します。