角の大きさ(20)　　　　 　　　　　　　　 　　　　　　　　　　　　　　　

　当ＨＰがいつもお世話になっているＨＮ「なつ」さんからの出題です。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和２年３月２０日付け）

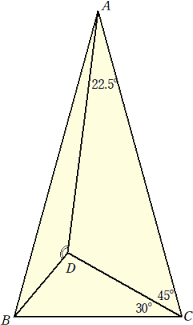△ABCの内部に点Dがあり、AB＝AC、∠ACD＝45°、 ∠BCD＝30°、∠CAD＝22.5°のとき、 ∠ADBの大きさを求めよ。

（答）　らすかるさんが考察されました。（令和２年３月２１日付け）

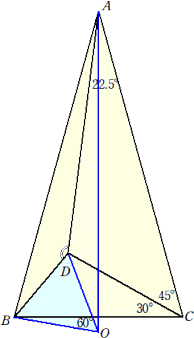直線BDに関して、Cがある側に△BODが正三角形となるよ うに点Oをとると、∠BCD=(1/2)∠BOD　なので、Oは△BCD の外接円の中心となる。 　すると、AOは∠CABの二等分線なので、ADは∠OABの二 等分線となり、直線ADはBOの垂直二等分線であることがわ かる。(※) 　従って、　∠ADB=180°-30°=150°　　（終）

(※)の証明：

　DからAB,AOに垂線DP、DQをおろすと、ADが∠OABの二等分線であることから、DP=DQ

　従って、△BDPと△ODQは斜辺と他の一辺が等しい直角三角形なので合同。

　△ADPと△ADQも合同なので、AB=AP+BP=AQ+OQ=AOからAD⊥BOとわかる。


（コメント）　△ＡＢＤと△ＡＯＤが合同になるとは．．．素晴らしい！


　なつさんからのコメントです。（令和２年３月２１日付け）

　感動しました…。美しすぎる…。こんな解き方あったんですね…。

　∠BDAと∠ODAが鈍角であることは言えるので、そこから直接、△ABDと△AODが合同っ
ていっちゃうのは強引なんですかね？


　らすかるさんからのコメントです。（令和２年３月２２日付け）

　テストの問題だったら、それでは減点されるでしょうね。「2辺が等しく挟まれた角が鈍角な
ら合同」と言えるわけではありませんので。（もっとスマートな示し方がある気がしますが）

　テストなら、私が「（※）の証明」で書いた程度は最低限必要でしょう。しかし、その証明でも
最後の部分は、はしょっていますので、テストの種類によっては、最後の部分をもう少しきち
んと書いた方が良いかも知れません。


　DD++さんからのコメントです。（令和２年３月２２日付け）

　今の場合は、「2辺とその間でない角がそれぞれ等しくて挟まれた角が鈍角」なので合同と
言えると思います。とはいえ結局証明はあった方がいいとは思いますけど。


　ＰＢさんからのコメントです。（令和２年３月２４日付け）

　おひさしぶりです。上記の問題について別解を考えました。

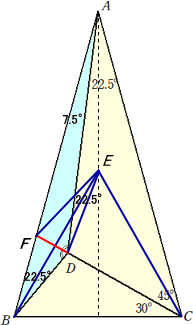△EBCが正三角形となるように、△ABCの内部に点Eをとる。 AEは、△ABCの対称軸となるので、 　　　∠BAD＝∠EAD＝7．5°・・・　(1) CDの延長とABの交点をFとする。CFも正三角形△EBCの対 称軸なので、　∠BFC＝∠EFC＝75° ・・・　(2) 　(1)(2)より、点Dは△AFEの傍心であり、EDは∠AEF(＝135°) の外角を二等分する。 　したがって、　∠FED(＝∠FBD)＝22．5°で、 　　△ABDの内角の和から、　∠ADB＝150°

＃傍心を使うのは珍しいと思い投稿しました。


（コメント）　いろいろな別解があって、上図に含蓄が相当あることが実感できました。
　　　　　　ＰＢさんに感謝します。