角の大きさ(18)　　　　 　　　　　　　　 　　　　　　　　　　　　　　　

　△ABCにおいて、∠Ｂ＝３８°、∠ＢＡＤ＝３３°、ＡＢ＝ＣＤ　とする。
このとき、∠Ｃの大きさを求めよ。

　　　



































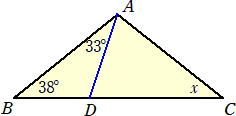
（答）　△ＡＢＤと合同な図形を裏返して辺CDに貼り付ける。

　　　

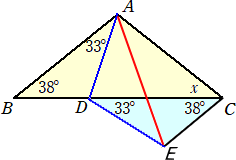
　このとき、　∠ＡＤＣ＝７１°より、　∠ＡＤＥ＝１０４°

　△ＡＤＥは２等辺三角形なので、∠ＤＥＡ＝∠ＤＡＥ＝（１８０°−１０４°）÷２＝３８°

　∠ＤＣＥ＝∠ＤＡＥ＝３８°で、両者とも線分ＤＥの同じ側にあるので、円周角の定理の逆より、

４点Ａ、Ｄ、Ｅ、Ｃは同一円周上にある。

　よって、　∠ＡＣＤ＝∠ＤＥＡ＝３８°　　（終）


　らすかるさんから別解をいただきました。（令和元年９月１２日付け）

（別解）　平行四辺形ABDEを作るとDC=DE、∠EDC=38°なので、

　　　∠ECD=(180°-38°)÷2=71°=∠ADC

　よって、四角形ADCEは等脚台形なので、　x=∠EDC=38°　（終）


（別解２）　∠AEB=∠ADC=71°となるようにBC上に点Eをとると、

　　　　∠EAB=180°-38°-71°=71°=∠AEB　なので、　CD=AB=BE

　　よって、　△ADC≡△AEB　なので、　x=∠ABC=38°　（終）


（コメント）　らすかるさんの解の方が自然で簡明ですね！策に溺れました．．．。


　よおすけさんからのコメントです。（令和元年９月１２日付け）

　∠Ｃが∠Ｂと等しい３８°ってことは、△ＡＢＣは二等辺三角形ですか？


　らすかるさんからのコメントです。（令和元年９月１２日付け）

　そうなりますね。