角の大きさ(17)　　　　 　　　　　　　　 　　　　　　　　　　　　　　　

　∠ＡＢＣ＝１５°、∠ＡＣＢ＝３０°の△ＡＢＣにおいて、下図のように、等脚台形AEBCを考
える。ただし、ＡＣ＝ＡＥ とする。ＡＣに垂直な線分ＡＤを引き、ＡＣ＝ＡＤ とする。

　　このとき、∠ＣＤＥの大きさを求めよ。

　　

































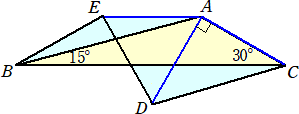
（答）　△ADCにおいて、ＡＣ＝ＡＤ、∠ＣＡＤ＝９０°から、∠ＡＤＣ＝４５°

　∠ＢＡＤ＝１８０°−１５°−３０°−９０°＝４５°

　∠ＢＡＥ＝∠ＡＢＣ＝１５°なので、　∠ＤＡＥ＝６０°

　ＡＥ＝ＡＤ　なので、∠ＡＤＥ＝６０°

　よって、　∠ＣＤＥ＝６０°＋４５°＝１０５°


　カルピスさんからのコメントです。（令和元年９月１０日付け）

　∠ＣＤＥには２つの答えが存在する。　１０５度　と　３６０−１０５＝２５５度

　「求める角度は、この図形の内部の角とする」の一文が入ってないと、２５５度でも正解か
な？