
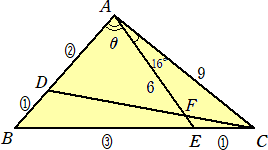
△ABCにおいて、辺ABを2:1に内分する点をD、辺BCを3:1に内分する点をEとする。
線分AEとCDの交点をFとすると、AF=6で、また、AC=9である。
∠CAF=16°のとき、∠DAF=θは何度になるか。
(灘中学校(2005年) 改題)
上図のままだけでは、解決の糸口は全く見えないが、巧妙に補助線を引くことにより鮮や
かに解かれる。難しいが、とても味のある問題だと思う。
(答) AEの延長上にAC=AGとなる点Gをとり、線分AGと平行に点Dより直線を引き、BG、
BCとの交点をそれぞれH、I とおく。
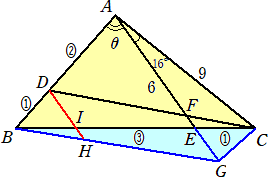
FG=3なので、AD:DB=AF:FG=2:1 より、DC‖BG
また、DH‖FG より、四角形DHGFは平行四辺形となる。
ここで、△BHI と△CFEにおいて、BI=CE、∠HBI=∠FCE、∠BIH=∠CEF なので、
△BHI ≡△CFE となり、 BH=CF
したがって、四角形BGCDは平行四辺形となり、 AB‖CG
よって、 16°+2θ=180°より、 θ=82° (終)
カルピスさんからのコメントです。(令和元年6月20日付け)
角度が「16度」しか与えられていない状態で、小学生が解けるということは、おそらく
(1) ∠Aが90度で、90−16=74度
または、
(2) 16度を頂点とする二等辺三角形が出来て、底角が82度
の、どちらかだなと容易に想像できる。
∠Aに用紙の角を当てると、用紙の角より大きいから、直角ではない。だから、答えは
82度と予想できる。
答えだけ書いても点数もらえるかな?
(コメント) カルピスさんのお察しの通り、(2)を意識しての作問でした。最後の詰めは、2等
辺三角形の底辺と辺ABが平行になるように、辺の長さや分点の比を与えること。
これは結構苦労しました!
DD++さんからのコメントです。(令和元年6月20日付け)
メネラウスの定理より、CF:FD=1:2 というのを使ってよければ、CG:GA=1:2 となる内
分点Gを取ることで、FG//AB かつ AF=AG となるので、あとは容易ですね。
#灘中の問題ってどこまで使っていいんだろうなあ。
(コメント) なるほど!CF:FD=1:2 、CG:GA=1:2 となる内分点Gを取って、2等辺三角形
を作った方が手っ取り早いですね。
愛犬ケンさんからのコメントです。(令和元年6月21日付け)
EAに平行な線分CGをとる。GはBAの延長線との交点とする。△ABE∽△GBC である。
また、△ADF∽△GDC で、相似比は、2:3 より、CG=9
△CAGは、頂角 C=16°の二等辺三角形なので、 θ=82°
#小学生はこう解くでしょう。
PBさんからのコメントです。(令和元年6月21日付け)
メネラウスの定理を用いなくても、この問題では、ABとBEの三等分点を順次結ぶことに
よって、CF:FD=1:2 が出せます。
とはいっても、メネラウス→高校 三角形の相似→中学 の範囲 ということで...。
灘中の問題は小学生の解く問題ですよね。
らすかるさんからのコメントです。(令和元年6月21日付け)
いろいろな解答が出ているようなので私も参加します。きっとこのように解く人もいるでしょう。
Dを通り、AEと平行な直線とBCの交点をGとすると、BG:GE:EC=1:2:1 となるので、
AE=3DG=9FE から、 AE=(9/8)AF=27/4
(使って良ければメネラウスの定理からAF/FE=(AD/DB)(BC/CE)=8としてもよい)
Eを通り、ABと平行な直線とACの交点をHとすると、 AH=(3/4)AC=27/4
よって、AE=AH なので、θ=∠AEH=(180°-16°)/2=82°
(コメント) 辺AC上に、AB//HE なる点Hをとると、△AEHが2等辺三角形になるという視座
は新発見です!らすかるさんに感謝します。