角の大きさ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

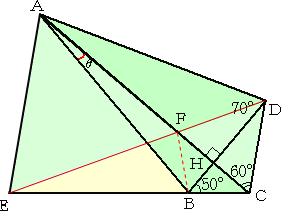
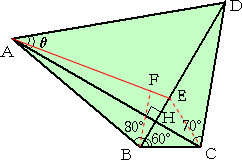
　下図の四角形において、角θは何度であろうか？

（１）
　　　　　　　　　　


（２）
　　　　　　　　　　　























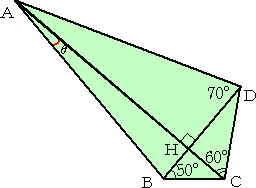
（答）　　１０°　（この問題は、ハンドルネーム tappon さんという方から頂きました。）

　　解答を得るために、次の等式を示す。

　　　　　　

　この等式は、

　


　

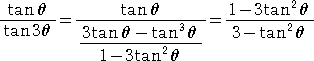
　から明らかであろう。

　　ところで、図（１）において、

　　　　ｔａｎ ２０°＝ＤＨ/ＡＨ　、ｔａｎ ３０°＝ＣＨ/ＤＨ　、ｔａｎ ４０°＝ＢＨ/ＣＨ

　なので、

　　　　ｔａｎ ２０°ｔａｎ ３０°ｔａｎ ４０°＝ＢＨ/ＡＨ＝ｔａｎ θ

　が成り立つ。

　　ところで、等式において、θ＝１０°とおくと、

　　　　ｔａｎ １０°＝ｔａｎ ２０°ｔａｎ ４０°ｔａｎ ３０°＝ｔａｎ ２０°ｔａｎ ３０°ｔａｎ ４０°

　が成り立つ。

　　したがって、　ｔａｎ θ＝ｔａｎ １０°より、θ＝１０°　となる。（　・・・・・　（１）の解　）

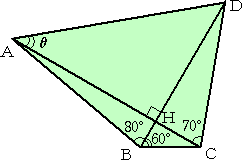
　（２）も同様に出来る。

　　図（２）において、

　　　　ｔａｎ １０°＝ＢＨ/ＡＨ　、ｔａｎ ２０°＝ＣＨ/ＤＨ　、ｔａｎ ６０°＝ＣＨ/ＢＨ

　で、さらに、

　　　　ｔａｎ θ＝ＤＨ/ＡＨ

　なので、

　　　　ｔａｎ θ　ｔａｎ ２０°＝（ＤＨ/ＡＨ）（ＣＨ/ＤＨ）＝ＣＨ/ＡＨ

　　　　ｔａｎ １０°ｔａｎ ６０°＝（ＢＨ/ＡＨ）（ＣＨ/ＢＨ）＝ＣＨ/ＡＨ

　　よって、

　　　　ｔａｎ θ　ｔａｎ ２０°＝ｔａｎ １０°ｔａｎ ６０°

　　ところで、等式において、θ＝２０°とおくと、

　　　　ｔａｎ ２０°＝ｔａｎ １０°ｔａｎ ５０°ｔａｎ ６０°

　なので、

　　　　ｔａｎ θ ＝１/ｔａｎ ５０°＝ｔａｎ （９０°−５０°）＝ｔａｎ ４０°

　が成り立つ。

　　したがって、　θ＝４０°　となる。（　・・・・・　（２）の解　）


（コメント：　この問題を初等的に解くことはできるのだろうか？）


（平成１６年１１月２０日追記）　ハンドルネーム tappon さんという方から、初等的な解法を
　　　　　　　　　　　　　　　　　　ご教示いただいた。

（１）
	点Ａより辺ＤＣに平行線を引き、辺ＣＢの 　　延長線との交点をＥ、線分ＥＤと対角線ＡＣ 　　の交点をＦとおく。 　　　このとき、四角形ＡＥＣＤは等脚台形なの 　　で、△ＡＥＦ、△ＤＣＦは正三角形である。 　　　よって、△ＢＤＣ≡△ＢＤＦ　より、 　　　　∠ＢＦＤ＝∠ＣＢＦ＝１００°　となる。 　　　このとき、△ＥＢＦは二等辺三角形で、 　　　　　ＥＢ＝ＥＦ＝ＥＡ　が成り立つ。 　　　よって、３点Ａ、Ｆ、Ｂは、点Ｅを中心とす 　　る同一円周上にある。 　　　したがって、 　　　　２θ＝∠ＢＥＦ＝２０°　より、θ＝１０°

（コメント：等脚台形を作るという発想に感動しました！補助線一発、まさに、幾何の醍醐味
　　　　　　が味わえますね。）

（２）
	対角線ＢＤ上に、△ＢＣＥが正三角形となるよう 　　に、点Ｅをとる。また、線分ＡＥ上に、ＢＥ＝ＢＦと 　　なるように、点Ｆをとる。 　　　このとき、△ＡＢＥは二等辺三角形で、 　　　　　∠ＢＥＦ＝∠ＢＦＥ＝８０°　となる。 　　　よって、△ＡＢＦと△ＤＢＣにおいて、 　　　　　ＢＦ＝ＢＣ、∠ＡＢＦ＝∠ＤＢＣ＝６０°、 　　　　　∠ＡＦＢ＝∠ＤＣＢ＝１００° 　　より、△ＡＢＦ≡△ＤＢＣ。　ゆえに、ＡＢ＝ＤＢ 　　　したがって、△ＢＡＤは二等辺三角形なので、 　　θ＋１０°＝∠ＢＤＡ＝５０°から、θ＝４０°

（コメント：ＡＢ＝ＤＢ　という事実には気がつきませんでした！）