角の大きさ（13）　 　　　　　　　　　　　　 　　　　　　　　　　　　　　　

　巷で話題になっていた問題として、なつさんからの出題です。（平成３１年３月２８日付け）

　先日ツイッターで話題になっていた問題です。皆さんどう解かれますか…？

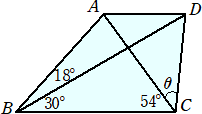
　四角形ABCDがあり、∠ABD＝18度、∠DBC＝30度、∠ACB＝54度、AD//BCのとき、
∠ACDを求めてください。

　　　































（答）　らすかるさんが考察されました。（平成３１年３月２９日付け）

　とりあえず解くには解きましたが、天下り的でしかも複雑なので、良い解答とは言えません。
もっと綺麗な解法があると思います。

(四角形ABCDがない状態から作図)

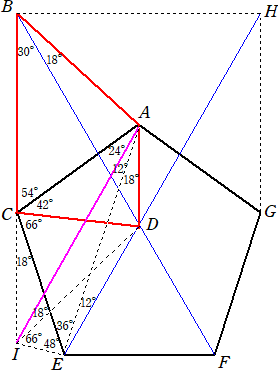正五角形ACEFGの内部に△DEFが正三角 　　形となるように点Dをとり、Cを通りADと平行な 　　直線と直線DFの交点をB、Gを通りADと平行 　　な直線と直線DEの交点をHとします。 　　　そして、∠AIB=30°となるようにBCのＣ側の 　　延長上に点 I をとります。 　∠BCA=∠DAC=54°なので、 　　　∠IAC=∠BCA-∠CIA=54°-30°=24° 　∠CEA=∠EAC=(180°-108°)÷2=36°より、 　　　∠EAI=∠EAC-∠IAC=36°-24°=12° 　また、∠CED=108°-60°=48°で、DE=EF=CE 　なので、∠DCE=(180°-48°)÷2=66°

　また、　∠AED=∠CED-∠CEA=48°-36°=12°

　△BDHは正三角形なので、AI=BD=BH=CG=AEであり、

　∠AIE=∠IEA=(180°-∠EAI)÷2=84°、∠IED=∠IEA+∠AED=84°+12°=96°

　∠ACD=108°-∠DCE=42°、∠DCI=180°-∠BCA-∠ACD=180°-54°-42°=84°

　∠IED+∠DCI=180°から四角形DCIEは円に内接しますので、∠DIE=∠DCE=66°

　∴∠AID=∠AIE-∠DIE=84°-66°=18°

　△ABD≡△DIAなので、∠ABD=∠AID=18°

　従って、∠ABD=∠AID=18°、∠DBC=30°、∠ACB=54°、AD//BCなので、

四角形ABCDは問題の四角形となり、∠ACD=42°です。


（コメント）　いや〜、難解ですね！


　カルピスさんからのコメントです。（平成３１年３月３０日付け）

　らすかるさん　凄いですね。私は方眼紙に正確に作図して分度器で測ってみました。
こんな幼稚な答えの出し方も「有り」かな？答えに辿り着くまでの道のりは、自由。。。


　しげるさんからのコメントです。（令和元年５月６日付け）

　らすかるさんの解答に拍手を送ります。少しだけ簡単に解けました。

　　
　
　ACとBDの交点をE、BC=a とします。∠BAC=78°で、△ABCに正弦定理を適用して、

　　AB=a*sin54°/sin78°=a*cos36°/cos12°

　さらに、∠BAD=132°で、sin132°=sin48°なので、△ABDに正弦定理を適用して、

　　BD=AB*sin132°/sin30°={a*(cos36°/cos12°)}*(sin48°/sin30°)

　また、∠BEC=96°で、sin96°=cos6°なので、△EBCに正弦定理を適用して

　　BE=a*sin54°/sin96°=a*cos36°/cos6°

　このとき、BE*BD=(BC^2) を示し、△BCE∽△BDC を証明します。

　BE*BD/(BC^2)

=(cos36°/cos6°)(cos36°/cos12°)(sin48°/sin30°)

=2(cos²36°)sin48°/(cos6°cos12°)

=2(cos²36°)(8sin6°cos6°cos12°cos24°)/(cos6°cos12°)

=16(cos²36°)(sin6°cos24°)

　ここで、２倍角の公式と積和の公式より、

　BE*BD/(BC^2)

=16(1/2)(1+cos72°)(1/2)(sin30°-sin18°)

=2(1+sin18°)(1-2sin18°)

=2-2sin18°-4(sin²18°)

=-{4(sin18°^2)+2(sin18°)-1}+1

　ここで、５倍角の公式から、sin5α=16(sin⁵α)-20(sin³α)+5sinα が言える。

実際に、

sin5α=sin（3α＋2α）

　　　=sin3αcos2α＋cos3αsin2α

　　　=（3sinα−4sin³α）（1−２sin²α）＋（4cos³α−3cosα）・2sinαcosα

　　　=（3sinα−4sin³α）（1−２sin²α）＋2sinα（4cos⁴α−3cos²α）

　　　=（3sinα−4sin³α）（1−２sin²α）＋2sinα（4（1−sin²α)²−3（1−sin²α)）

　　　=16(sin⁵α)-20(sin³α)+5sinα

　そこで、α=15°として、　sin90°=16(sin⁵18°)-20(sin³18°)+5sin18°

　x=sin18°とおくと、　sin90°=1　なので、　16x^5-20x^3+5x-1=0

因数分解して、　(x-1)(4x^2+2x-1)^2=0

　ここで、　x≠1　なので　4x^2+2x-1=0　すなわち、　4(sin18°^2)+2(sin18°)-1=0

　以上から、　BE*BD/(BC^2)=1　すなわち、　BE/BC=BC/BD　となり、∠ＣＢＤ共通で、

△BCE∽△BDC　が言えます。

　よって、∠BDC=∠BCE=54°となり θ=∠BEC-∠BDC=96°-54°=42°となります。


（コメント）　三角関数の諸公式を駆使した見事な解答ですね！感動的です。


　ＧＡＩ さんからのコメントです。（令和元年５月１１日付け）

　他の角度の問題で同じ問題が作れないか調べてみた。

（１）　∠ABD=50°、∠DBC=30°、∠ACB=40°の時、∠ACD=70°

（２）　∠ABD=90°、∠DBC=30°、∠ACB=30°の時、∠ACD=90°

（３）　∠ABD=126°、∠DBC=30°、∠ACB=18°の時、∠ACD=114°

　一般に、-44≦i≦44 のとき、

　∠ABD=｜(45-3*i)｜°、∠DBC=(45+i)°、∠ACB=(45+i)°の時、∠ACD=｜(45-3*i)｜°

が起こりそうです。

　整数の角度で問題設定できるものは限られており、特に、∠DBC=30°の場合が冒頭の
問題と合わせて、４タイプ構成可能でした。

　他は、∠DBC=54°でも、３タイプ構成可能でした。

（イ）　∠ABD=18°、∠DBC=54°、∠ACB=54°の時、∠ACD=18°

（ロ）　∠ABD=84°、∠DBC=54°、∠ACB=30°の時、∠ACD=66°

（ハ）　∠ABD=96°、∠DBC=54°、∠ACB=24°の時、∠ACD=78°


　ＰＢさんからのコメントです。（令和元年５月１４日付け）

　GAIさんのコメントの

　一般に、-44≦i≦44 のとき、
　∠ABD=｜(45-3*i)｜°、∠DBC=(45+i)°、∠ACB=(45+i)°の時、∠ACD=｜(45-3*i)｜°

についてですが、

　∠DBC=∠ACB　であれば、AD//BC　より、∠DAC=∠DBC　が成り立ち、四角形ABCD は
円に内接するので、∠ABD=∠ACD　です。（さらに一般の場合で成り立ちます）

　（２）　∠ABD=90°、∠DBC=30°、∠ACB=30°の時、∠ACD=90°

については、これにより成立します。その他の問題については、とりあえず

（１）　∠ABD=50°、∠DBC=30°、∠ACB=40°の時は、点Aの直線BDに関しての対称点A’

をとれば、ABA’Dは凧形で、∠ADA’=60°より、△AA’Dは正三角形となり、AA’=AD　…　(*)

　∠ABD=∠A’BD=50°および　AA’⊥BD　より、∠A’BC=∠A’AC=20°であるから、

四角形ABA’Cは円に内接し、∠BCA’=∠BAA’=40°

　これより、∠ACA’=∠AA’C=80°　したがって　AA’=AC　…　(**)

　(*)(**)より、点Aは、△CDA’の外心であり、円周角と中心角の関係から、

　∠A’DC=(1/2)∠A’AC=10°、∠DA’C=(1/2)∠DAC=20°

　以上により、三角形の内角の和から、∠ACD=70°　が成り立つ。

＃　他の問題については、現在考え中…。解けたら送りたいと思います。


　ＰＢさんからのコメントです。（令和元年６月４日付け）

　だいぶ時間がたってしまいましたが、GAIさんの問題ができました。当初の問題の、らすか
るさんの解答を参考に作りましたが、だいぶ複雑になってしまいました。

　とりあえず、以下のようにして解きました。



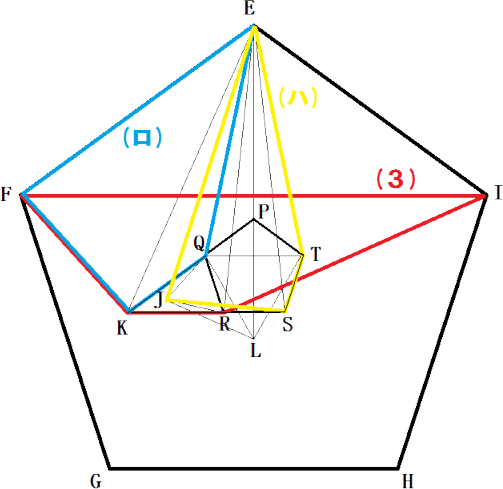
（解）　正五角形EFGHIの内部に△PGHが正三角形となるように点Pをとる。同様に、４つの
　　　正三角形　△QHI、△RIE、△SEF、△TFGをつくれば、PQRSTも正五角形となる。

　ここで、外側の正五角形の頂点Eと小正五角形の各頂点を結ぶと、

　∠TEF＝66°（頂角108°−60°＝48°の二等辺三角形△EFTの底角）
　∠SEF＝60°（△SEF　は正三角形）
　∠PEF＝54°（正五角形の内角の1/2）　および、対称性により
　∠TES＝∠SEP＝∠PER＝∠REQ＝6°　である。

　なお、このことはEFGHIの他の頂点から、PQRSTを結んだ場合についても成り立つ。

（※）　△JRQが正三角形となるように点Jを取ると、∠QEJ=6°である

*************************************
（※）の（証明）　　△ERSが頂角12°の二等辺三角形であるから　∠ERS＝84°
　∠ERQ＝108°−84°＝24°　より　∠ERJ＝24°＋60°＝84°
　JR＝RS　であるから　二辺夾角相等により　△ERJ≡△ERS
　したがって、△ERJも頂角12°の二等辺三角形であり、EQはその対称軸
　よって、∠REQ＝∠QEJ＝6°　（証終）
*************************************


（※※）　PQとSRの延長の交点をKとすると∠JEK＝6°である

*************************************
　（※※）の（証明）　△KRQと△TQRはいずれも底角72°の二等辺三角形であり、底辺QR
　が共通なので、△KRQ≡△TQR　よって、KQ＝QT
　いま、JR＝QR　であるから、△KRQ　と合同な　△LQJをFの反対側に作図する。
　QL＝QT　および、∠LQT＝∠PQR−∠PQT−∠LQR＝108°−36°−12°＝60°
　であるから　△QLT　は正三角形であり、四角形EQLTは凧形
　よって、点Pは、その対称軸EL上にある。
　∠EQK＝∠EQL＝138°　KQ＝LQ　であるから、二辺夾角相等により　△EQK≡△EQL
　よって、∠QEK＝∠QEL＝∠QEP＝12°から　∠JEK＝6°　（証終）
*************************************

　このとき、

○EL同様、KIも二つの正五角形の共通の対称軸であり、K、J、T、I は、同一直線上にある。

○PK//EF　より∠EKP＝∠KEF＝30°、△QKRの頂角　∠QKR＝36°より、
　∠EKR＝66°＝∠EFR　から、四角形EFKRは円に内接する。

　以上を踏まえて、

（３）　∠ABD=126°、∠DBC=30°、∠ACB=18°の時、∠ACD=114°

（解答）　図において、I→A、R→B、K→C、F→D　とすれば、

　　∠IRF＝∠IRE＋∠ERF＝60°＋66°＝126°

　　∠KRF＝∠KEF＝30°（四角形EFKR　は円に内接）

等により、四角形ABCDは(３)の条件を満たし、四角形EFKRが円に内接することから、

　∠KFR＝∠KER＝18°

　△IFKの内角の和から、　∠ACD＝∠IKF＝114°である．

（ロ）　∠ABD=84°、∠DBC=54°、∠ACB=30°の時、∠ACD=66°

（解答）　図において、E→A、Q→B、K→C、F→D　とすれば、FQが正五角形の対称軸であ

　　　　ることから、∠EFQ＝54°

　　また、∠FEK＝30°　EF//QK　等により、四角形ABCDは(ロ)の条件を満たし、EFKRが

円に内接するので、∠ACD＝∠EKF＝∠ERF＝66°である。

（ハ）　∠ABD=96°、∠DBC=54°、∠ACB=24°の時、∠ACD=78°

（解答）　図において、E→A、T→B、S→C、J→D　とすれば、∠FEJ＝36°＝∠FEG　より

　　　　Jは線分EG上にあり　EJ//TS、TJが正五角形の対称軸であるから　∠JTS＝54°

　　　　∠JTE＝（∠JTP−∠QTP）＋∠QTE＝（54°−36°）＋78°＝96°

　　であること等により、四角形ABCDは(ハ)の条件を満たし、△EJSが頂角24°の二等辺

　　三角形であることから、∠ACD＝∠ESJ＝78°である。

（＃）　図は一つにまとめるため、省略した線分があります。(複雑になりすぎるため…)証明
　　　についても同様ですが、それでもかなりの長さなので、必要に応じて補足またはカット
　　　して下さい。なお、(３)の解答は、当初のらすかるさんの図において、DEとBCの交点を
　　　Jとして、J→A、D→B、A→C、B→D と置き換えてもできます。