
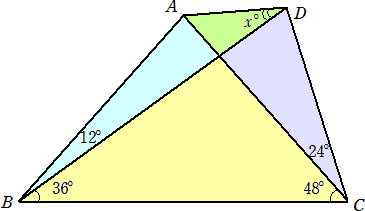
下図において、∠ADB=x°の大きさを求めよ。
(答) △ABDをABに関して対称移動させて正三角形EBCを作る。
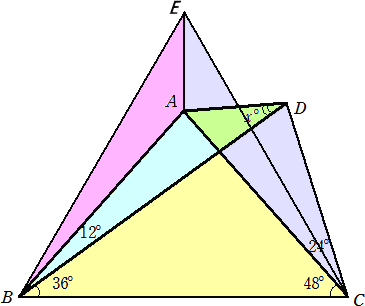
∠CBD=36°、∠BCD=72°なので、∠BDC=180°−36°−72°=72°
よって、△BCDは、BC=BDの2等辺三角形
正三角形EBCの作り方から、 BD=BE
また、∠ABC=48°、∠ACB=48°より、△ABDはAB=ACの2等辺三角形
このとき、△EAC≡△DAB≡△EAB なので、 2x=60 より、 x=30(度)
(コメント) 正三角形が思いつくかどうかですね...。
らすかるさんから別解をいただきました。(平成30年10月19日付け)
ABに関してCと対称な点C’をとると、△ABC≡△ABC’なので、AB=AC’
BD=BC=BC’、∠C’BD=60°から、△BDC’は正三角形なので、BD=C’D
従って、AもDもBC’の垂直二等分線上にあり、∠ADB=30°
(コメント) なるほど!そちらにも正三角形が作れるんですね。