
下図において、α、βの角の大きさを求めよ。
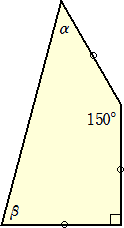
(答) 下図のように、正方形ABCDと正三角形ADEを作図すると、△ABEは、AB=AEの2
等辺三角形となる。
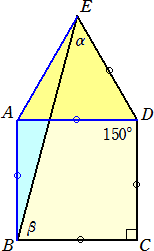
よって、 α=60°−(180°−150°)/2=45°
β=90°−(180°−150°)/2=75°
DD++ さんから別解をいただきました。(平成30年8月29日付け)
角の大きさ(11) 
下図において、α、βの角の大きさを求めよ。

(答) 下図のように、正方形ABCDと正三角形ADEを作図すると、△ABEは、AB=AEの2
等辺三角形となる。

よって、 α=60°−(180°−150°)/2=45°
β=90°−(180°−150°)/2=75°
DD++ さんから別解をいただきました。(平成30年8月29日付け)
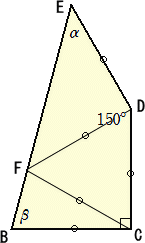 |
B、C、D、E の点の名前は管理人さんのを使います。 正三角形 CDF を辺 CD の左に取ります。DE=DF と ∠EDF=90° から、∠DEF=∠DFE=45° CB=CF と ∠BCF=30° から、∠CBF=∠CFB=75° ここで、∠DFE+∠DFC+∠CFB=45°+60°+75°=180° つまり、E、F、B は実は一直線上にあるので、α=45°、β=75° |
S(H)さんから別解をいただきました。(平成30年8月29日付け)
B(-1, 0)、C(0, 0)、D(0, 1)、E(-1/2, 1 + Sqrt[3]/2) と4点を定めて構わない。
BEを通る直線は、 y = 2 + Sqrt[3] + (2 + Sqrt[3]) x で、Tan[β]= (2
+ Sqrt[3])
このとき、β=(5*π)/12
また、 Pi/2 + (5*π)/6 +α + (5*π)/12 = 2*Pi から、α=π/4
らすかるさんから別解をいただきました。(平成30年8月29日付け)
流行っているようなので私も...。B、C、D、E の点の名前は管理人さんのを使います。
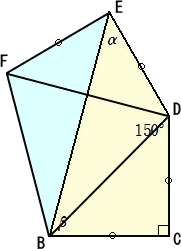 |
△DEFが直角二等辺三角形となるように点Fをとります。ただし、 点Fは線分DFが線分BEと交わるようにとります。 ∠FDE=∠CDB=45°なので、∠BDF=150°-45°-45°=60° △DEF≡△BCD から、BD=DF なので、△BDFは正三角形 となり、四角形BDEFは凧形ですから、BEはDFの垂直二等分 線とわかります。 従って、α=∠DEF÷2=45°、β=∠FBD÷2+∠DBC=75° |
さらに、らすかるさんから別解をもう一ついただきました。
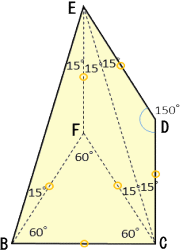 |
*左図は、tetsuさんよりご提供いただきました。 (平成30年8月30日付け) |
菱形CDEFを作ると、△BCFは正三角形となり、EがBCの垂直二等分線上にあることがわ
かるので、 ∠BFE=∠CFE=150°から、∠FEB=∠FBE=15°
よって、 α=∠DEF+∠FEB=45°、β=∠FBE+∠FBC=75°
S(H)さんから別解をいただきました。(平成30年8月30日付け)
もう流行らせたくないので、トドメの瞬殺法を...。
B(-1, 0)、C(0, 0)、D(0, 1)、E(-1/2, 1 + Sqrt[3]/2) と4点を定めて構わない。
補助線など全然引かず視た通りで、BCを回してk倍して、
k*({{Cos[t], -Sin[t]}, {Sin[t], Cos[t]}}.(({0, 0} - {-1, 0}))) = {-(1/2),
1 + Sqrt[3]/2} - {-1, 0}
から不要なのを消して、 {t,k} = {(5*π)/12, Sqrt[2 + Sqrt[3]]} で、 β=(5*π)/12
Pi/2 + (5*π)/6 +α + (5*π)/12 = 2*Pi から、α=π/4
また、補助線など全然引かず、視たままでも解ける。
△BDEの高さは、 Sqrt[2 + Sqrt[3]]*Sin[β] = 1 + Sqrt[3]/2 から、β=(5*π)/12
Pi/2 + (5*π)/6 +α + (5*π)/12 = 2*Pi から、α=π/4
さらに、次のようにしても解ける。
△BCEに余弦定理を使い、
(Sqrt[2 + Sqrt[3]])^2 = (Sqrt[2 + Sqrt[3]])^2 + 1^2 - 2*(Sqrt[2 + Sqrt[3]])*(1)*Cos[β]
から、 β=(5*π)/12
Pi/2 + (5*π)/6 +α + (5*π)/12 = 2*Pi から、α=π/4
よおすけさんからのコメントです。(令和元年9月15日付け)
この問題は、1993年の算数オリンピック予選問題8です。
よおすけさんからのコメントです。(令和6年8月17日付け)
6年前にUPの問題で、新たな視点から考察してみました。
下図の四角形ABCDにおいて、
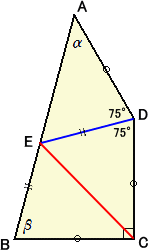
Dから辺ABへ、および、Cから辺ABへそれぞれ角の二等分線を引いた各交点は一致する
ので、E とする。
これより、∠CDE=∠ADE=75°、∠BCE=∠DCE=45°
また、BC=CD=DA および、BE=DE なので、△BCE≡△DCE≡△DAB より、
∠BCE=∠DCE=∠DAE、∠CDE=∠ADE=∠CBE
以上から、α=∠DAE=45°、β=∠CBE=75°
(コメント) 「Dから辺ABへ、および、Cから辺ABへそれぞれ角の二等分線を引いた各交点
は一致する」が、α=45°、β=75°ならば、結果としてそうなるんだけれども、これ
が追認できませんでした。よおすけさん、証明をお願いします。
よおすけさんからのコメントです。(令和6年8月20日付け)
厳密にはできませんでしたが、元の問題が1993年の算数オリンピック予選問題ということで、
中学生以下の範囲で以下のようにやってみました。
四角形ABCDにおいて、BC=CD=DAだから、
・ADをCDに重なるように折り曲げる。
・BCをDCに重なるように折り曲げる。
上2つの折り曲げた部分の三角形は重なるので、α=45°、β=75°
(コメント) α=45°、β=75°ならば、上2つの折り曲げた部分の三角形は重なるので
すが...?証明は難しいですね!
冒頭の解答のように、「α=45°、β=75°」を示してから、実は、上2つの折り曲げた
部分の三角形は重なるので、∠Cと∠Dの2等分線はAB上で交わるという性質を持つんだ
というスタンスで、納得しましょう。
以下、工事中!